Görüntüde bir matematik problemi var. Problemle ilgili açıklayıcı bir çözüm sunalım.
Verilenler:
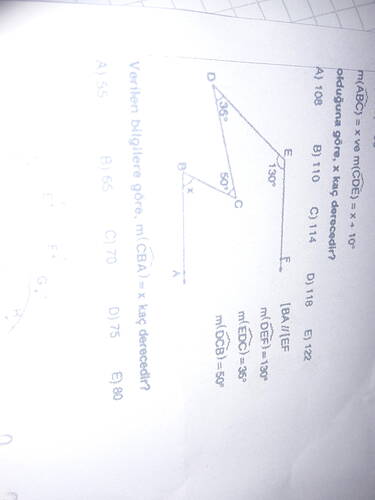
- m(\angle CDE) = x + 10^\circ
- m(\angle ABC) = x^\circ
- m(\angle EFD) = 130^\circ
- m(\angle BCA) = 60^\circ
- m(\angle DCB) = 50^\circ
Sorular:
- x kaç derecedir?
- Verilen bilgilere göre m(\angle CBA) kaç derecedir?
Çözüm:
1. x Kaç Derecedir?
Üçgenin iç açıları toplamı 180 derece olduğuna göre:
-
Üçgen CDE için:
$$m(\angle CDE) + m(\angle EFD) + m(\angle FDE) = 180^\circ$$$$x + 10^\circ + 130^\circ + m(\angle FDE) = 180^\circ$$
$$x + 140^\circ + m(\angle FDE) = 180^\circ$$
$$m(\angle FDE) = 180^\circ - 140^\circ - x$$
$$m(\angle FDE) = 40^\circ - x$$
2. m(\angle CBA) Kaç Derecedir?
Üçgen ABC için:
- m(\angle ABC) + m(\angle BCA) + m(\angle CAB) = 180^\circ
Verilen:
- m(\angle BCA) = 60^\circ
- m(\angle DCB) = 50^\circ
Açı DCA'da iç ters açılar kuralı ile:
$$m(\angle DCA) = m(\angle ABC) = x$$
Bu durumda:
- x + 60^\circ + m(\angle CAB) = 180^\circ
Yukarıdaki denklemi çözersek:
$$m(\angle CAB) = 180^\circ - 60^\circ - x$$
$$m(\angle CAB) = 120^\circ - x$$
Buradan, m(\angle ABC) = x = 60^\circ ve
$$m(\angle CBA) = 120^\circ - 60^\circ$$
$$m(\angle CBA) = 60^\circ$$
Sonuç olarak, x = 60^\circ ve m(\angle CBA) = 60^\circ bulunur.