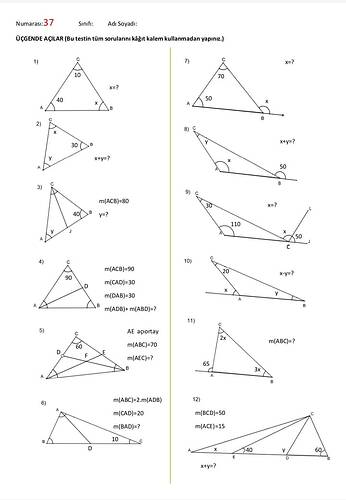
11. ve 12. Soruların Çözümü:
11. Soru: m(ABC)=?
Soruda verilenler:
- \text{m(A)} = 65^\circ ,
- \text{B noktasındaki açının ölçüsü} = 3x,
- \text{C noktasındaki açının ölçüsü} = 2x.
Bir üçgende iç açılar toplamı her zaman 180^\circ'dir. Yani:
\text{m(A)} + \text{m(B)} + \text{m(C)} = 180^\circ
Denklemi yerine koyalım:
65^\circ + 3x + 2x = 180^\circ
Düzenleyelim:
65^\circ + 5x = 180^\circ
Her iki taraftan 65^\circ çıkaralım:
5x = 115^\circ
Her iki tarafı 5’e bölelim:
x = 23^\circ
Şimdi x'i yerine koyarak m(B) ve m(C)'yi bulalım:
- \text{m(B)} = 3x = 3 \cdot 23^\circ = 69^\circ,
- \text{m(C)} = 2x = 2 \cdot 23^\circ = 46^\circ.
Sonuç:
m(ABC) = \text{m(A)} + \text{m(B)} + \text{m(C)} = 65^\circ + 69^\circ + 46^\circ = 180^\circ
Cevap:
m(ABC) = 180^\circ
12. Soru: x + y = ?
Soruda verilenler:
- \text{m(BCD)} = 50^\circ,
- \text{m(ACE)} = 15^\circ,
- \text{D ve E noktalarındaki x ve y değerlerini bulmamız isteniyor}.
Adım 1: Üçgende dış açılar
Bir üçgenin dış açısı, kendisine komşu olmayan iki iç açının toplamına eşittir. Örneğin, \text{m(BCD)}, üçgen \Delta ABE'de x ve 40^\circ'nin toplamına eşit olur.
\text{m(BCD)}:
\text{m(BCD)} = x + 40^\circ
Verilen \text{m(BCD)} = 50^\circ olduğuna göre:
50^\circ = x + 40^\circ
Her iki taraftan 40^\circ çıkaralım:
x = 10^\circ
Adım 2: \text{m(ACE)} Açısı
Benzer bir şekilde, \text{m(ACE)}, üçgen \Delta CED'de y ve 60^\circ'nin toplamına eşittir.
\text{m(ACE)}:
\text{m(ACE)} = y + 60^\circ
Verilen \text{m(ACE)} = 15^\circ olduğuna göre:
15^\circ = y + 60^\circ
Her iki taraftan 60^\circ çıkaralım:
y = -45^\circ