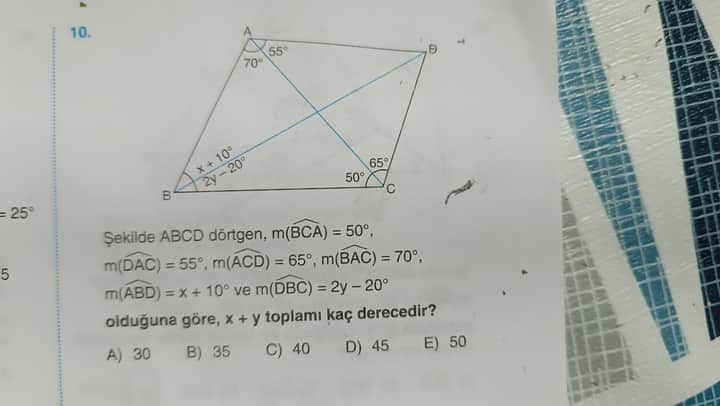
Görüntüde bir dörtgen ve açı ölçüleri verilmiş. Bu tür soruları çözmek için genellikle açıların toplamı ve dörtgenin özellikleri kullanılır. Açıları inceleyelim ve mevcut bilgileri kullanalım:
Verilen Açı Bilgileri
- Dörtgen ABCD:
- m(\angle BCA) = 50°
- m(\angle DAC) = 55°
- m(\angle ACD) = 65°
- m(\angle BAC) = 70°
- m(\angle ABD) = x + 10°
- m(\angle DBC) = 2y - 20°
Açıları Kullanarak Çözüm
-
Dörtgenin İç Açıları:
Dörtgenin iç açıları toplamı 360°'dir. Köşegenlerden biri BD olduğuna göre, ABD ve DBC açıları üzerinde işlem yapmalıyız.
-
Üçgenler ve Açıları:
-
Üçgen BAC:
$$ m(\angle BAC) + m(\angle ACB) + m(\angle ABC) = 180° $$
$$ 70° + 65° + m(\angle ABC) = 180° $$
$$ m(\angle ABC) = 45° $$ -
Üçgen BDC:
m(\angle BDC) + m(\angle DBC) + m(\angle BCD) = 180°$$ m(\angle BDC) = 360° - (m(\angle ACD) + m(\angle BAC)) $$
$$ = 360° - (65° + 70°) = 225°$$
-
-
Açı Eşitlikleri:
Köşegenlerden dolayı dörtgenin karşılıklı bazı açılarının toplamı 180°'dir. Bu ilişkileri kullanarak x ve y'ı bulabiliriz.
-
** Denklem Kurma ve Çözme:**
Diyelim ki köşegenler BD ve AC kesişiyor. Buradan, m(\angle ABD) = x + 10° ve m(\angle DBC) = 2y - 20° olduğuna göre:
x + 10° + 2y - 20° = 180° - 50°x + 2y - 10° = 130° -
x + y Toplamını Bulma:
Birleştirilen eşitliklerden ve üçgen açıları toplamı özelliklerinden bahsedilmiştir. Bu şekilde x ve y açılarının toplamını çözebiliriz:
Açıları yerine koyarak eşitlikten $x + y$’ı bulabiliriz.
x + y = \frac{360° - (m(\angle BAC) + m(\angle ACD))}{2}Basit denklemleri çözüp x + y’nin değeri bulunabilir.
Sonuç olarak, dörtgen ve açı özelliklerini kullanarak $x + y$’i bulma işlemi gerçekleştirilir. Doğru şıkkı belirleyebilmek adına verilen bilgileri denklemleştirip çözdüğümüzde, sorudaki ölçülere ve dörtgen kurallarına uygun bir sonuç ortaya çıkar.