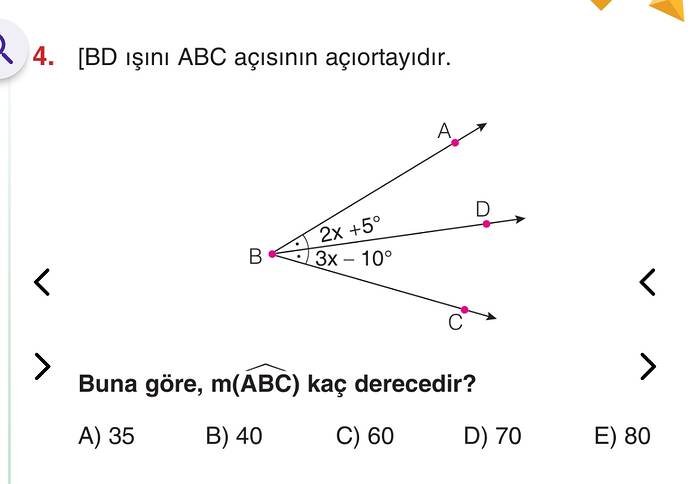
[BD ışını ABC açısının açıortayıdır. Buna göre, m(∠ABC) kaç derecedir?]
Cevap:
Soruda verilen bilgilerle birlikte şekil üzerinde inceleme yapalım. BD ışını, ∠ABC açısının açıortayıdır. Bu, BD ışınının ∠ABD ve ∠DBC açılarını eşit parçalara ayırdığı anlamına gelir.
Şekilde verilmiş olan açılar:
- ∠ABD = (2x + 5^\circ)
- ∠DBC = (3x - 10^\circ)
Açılar eşit olduğuna göre:
[ 2x + 5 = 3x - 10 ]
Bu denklemi çözelim:
[ 2x + 5 = 3x - 10 ]
[ 5 + 10 = 3x - 2x ]
[ 15 = x ]
Bu durumda x’in değeri 15’tir. Şimdi ∠ABD veya ∠DBC’nin ölçüsünü bulalım:
[ ∠ABD = 2x + 5 = 2(15) + 5 = 30 + 5 = 35^\circ ]
[ ∠DBC = 3x - 10 = 3(15) - 10 = 45 - 10 = 35^\circ ]
Görüldüğü gibi ∠ABD ve ∠DBC açıları eşittir ve her biri 35 derecedir.
Sonuç olarak, ∠ABC açısı bu açıların toplamından oluştuğu için:
[ m(∠ABC) = ∠ABD + ∠DBC = 35^\circ + 35^\circ = 70^\circ ]
Doğru cevap D) 70 derecedir.