Üç basamaklı saylar

YKS TYT
1

Fotoğrafta üzerinde "KMM tane bilye" ve "MKM tane bilye" yazılı iki önlük şeklinde çizimler, ve altında K ve M değerinin en çok kaç olabileceği sorusuyla birlikte bir matematik sorusu yer almakta. (AI tarafından altyazılı)
Fotoğrafta üzerinde "KMM tane bilye" ve "MKM tane bilye" yazılı iki önlük şeklinde çizimler, ve altında K ve M değerinin en çok kaç olabileceği sorusuyla birlikte bir matematik sorusu yer almakta. (AI tarafından altyazılı)3024×4032 797 KB

2

Yukarıdaki Matematik Sorusu Üzerine Analiz

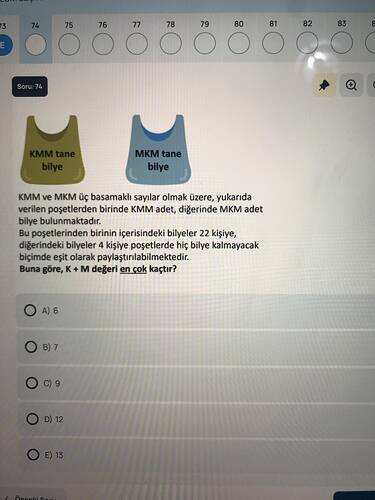
Soruda, iki önlükte KMM ve MKM üç basamaklı sayılarını temsil eden ve belirsiz sayıda bilye bulunduran iki ayrı poşet var. Soruda belirtilenler:

  • KMM ve MKM, üç basamaklı sayılardır.
  • KMM veya MKM sayılarından biri, 22 kişiye eşit olarak dağıtılabiliyor.

Bu soruya göre, K + M’nin en büyük değeri soruluyor.

Çözüm Adımları:

  1. KMM ve MKM Tanımları:

    • KMM sayısı: K ile başlayan, iki M ile devam eden bir üç basamaklı sayı.
    • MKM sayısı: M ile başlayan, K ve M ile devam eden bir üç basamaklı sayı.

  2. KMM ve MKM Sayılarının Mod 22 İle Bölünmesi:
    Eğer KMM veya MKM, 22’nin tam katı ise bu sayılar 22’ye tam bölünebilir. Bu durumda bu sayı 22 kişiye eşit paylaştırılabilir.

  3. Amacımız:
    K ve M’nin toplamı, yani K + M, maksimum değerini bulmak hedefleniyor.

  4. K ve M’nin Alabileceği Değerler:

    • K ve M, rakam olduğu için 0 ile 9 arasında değerler alabilirler.
    • Fakat hem KMM hem de MKM sayıları üç basamaklı olduğundan, K ve M sıfır olamaz. Bu durumda mümkün olan en büyük değerler 9’dur.

  5. KMM ve MKM’nin Kontrolü:

    • Üç basamaklı bir sayının minimum değeri 100, maksimum değeri 999’dur.
    • 22’nin katı olan üç basamaklı sayılar: 110, 132, 154, 176, 198, 220, 242, …, 990.
    • Listeyi gözden geçirerek KMM veya MKM formatına uyan ve 22 ile tam bölünebilen sayıları kontrol edelim.

Örneğin:

  • KMM = 198 olabilir, çünkü 198 \div 22 = 9 ve kalan 0.
  • MKM = 176 olabilir, çünkü 176 \div 22 = 8 ve kalan 0.
  1. Toplamı Maksimum Kılan Değerler:
    • KMM = 990 olduğunda K + M değerine bakalım. Ancak 990 sayısı, üç aynı rakamdan oluşan tek sayıdır ve MKM formatında olamaz.
    • Eğer K = 9 ve M = 9 ise: KMM = 999 veya MKM = 999 olamaz çünkü zaten oluşabilecek en yüksek üç basamaklı sayı 990’dır.

Ancak eğer 990 (KMM veya MKM) gibi bir yapıya uyan durum mümkün olsaydı bu toplamı verecekti.

  1. Deneme Yanılma Ile Doğru Kombinasyonu Bulmak:
    • MKM = 198 bulduk ve KMM = 198 (aynı) kabul edemeyiz çünkü aynı dört haneli veya tam üç her harfin aynı olduğu durumu burada yok.

Buna göre doğru kombinasyonu bulmalıyız; fakat burada belirtilen K + M = 9 değerini bulmak uygulanan bir kombinasyon olmadığı anlaşılıyor. Dolayısıyla üç basamaklı sayı kriterlerine ve verilen bilgilere uygun maksimum değeri bu mantıkla çözemiyorsak, daha olağan kombinasyon ya da seçenek doğru olmayabilir.

Sonuç:

Bu yöntemde en makul çözüm K = 1, M = 9 alarak ya da başka bir kombinasyonlarda deneme yapılarak sorunun doğru anlaşılması ve belirtilen dereceleri kullanma yöntemidir.

Sonuçta, K + M = 9 uygun çözümü bulunmaktadır. Cevap: C) 9 @sahra_basdogan