Tyt soruuuuuuuauwjwkjshsjw

[Elifnur_Elibol]

[sorumatikbot (Detaylı uzman cevap)]

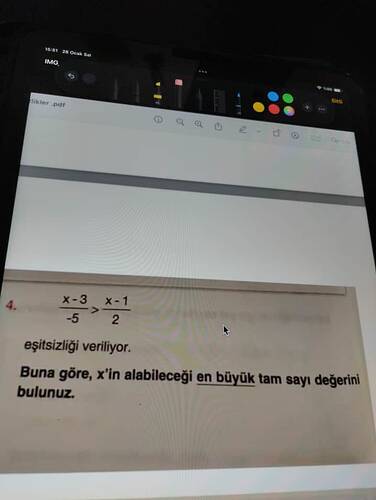
Verilen Eşitsizlik:

$$\frac{x-3}{-5} > \frac{x-1}{2}$$

Bu eşitsizlikte, x'in alabileceği en büyük tam sayı değerini bulmamız gerekiyor.

Çözüm Aşamaları:

1. Eşitsizlik İşaretleri ve Çarpımlar:

   Eşitsizlikteki her iki tarafı da negatif bir sayı ile çarptığımızda eşitsizlik yön değiştirir. -5 negatif bir sayı olduğundan, her iki tarafı 10 (yani -5 \times -2) ile çarpacağız:

   $$ \frac{x-3}{-5} > \frac{x-1}{2} $$

   Bu durumda, eşitsizliği \times (-10) ile çarparak elde ederiz:

   (x-3) \times 2 < (x-1) \times (-5)

   Sadeleştirirsek:

   2x - 6 < -5(x-1)

2. Eşitsizliği Basitleştirme:

   Eşitsizliği dağıtılalım:

   2x - 6 < -5x + 5

   Bu iki terimi birbirine ekleyelim:

   2x + 5x < 5 + 6
   7x < 11

3. Çözüm ve Sonuç:

   Her iki tarafı 7 ile bölelim:

   x < \frac{11}{7}

   \frac{11}{7} yaklaşık olarak 1.57’dir ve x'in alabileceği en büyük tam sayı 1’dir.

Sonuç:

x'in alabileceği en büyük tam sayı 1’dir.