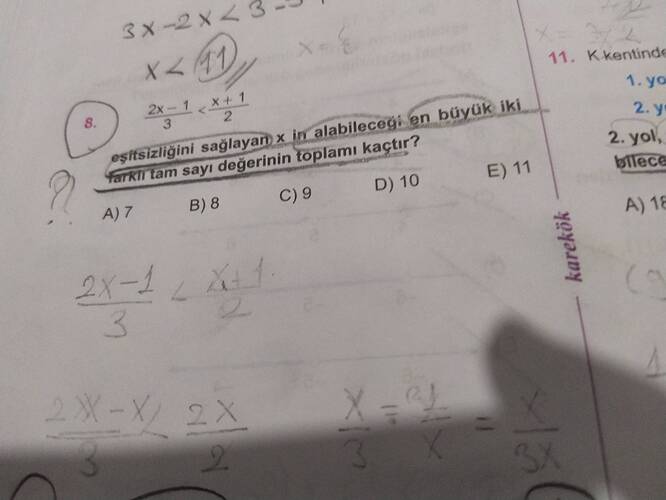Görseldeki soruyu çözmek için eşitsizliği çözmemiz gerekiyor. Soruda verilen eşitsizlik:
$$ \frac{2x - 1}{3} < \frac{x + 1}{2} $$
Bu eşitsizliği çözmek için adım adım ilerleyelim:
Adım 1: Eşitsizliği Genişletin
Öncelikle kesirlerden kurtulmak için her iki tarafı da ortak paydayla çarpalım. Burada ortak payda 6’dır. Bu nedenle, eşitsizliğin her iki tarafını da 6 ile çarpalım:
$$ 6 \cdot \frac{2x - 1}{3} < 6 \cdot \frac{x + 1}{2} $$
Bu, eşitsizliği şu hale getirir:
$$ 2(2x - 1) < 3(x + 1) $$
Adım 2: Dağıtın
Her iki tarafı da dağıtalım:
$$ 4x - 2 < 3x + 3 $$
Adım 3: x’i İzole Edin
Şimdi x'i izole etmeye çalışalım. İlk olarak 3x'i diğer tarafa taşıyalım:
$$ 4x - 3x - 2 < 3 $$
Bu işlemi gerçekleştirdikten sonra:
$$ x - 2 < 3 $$
Sonra her iki tarafa da 2 ekleyelim:
$$ x < 5 $$
Adım 4: $x$’in Tam Sayı Değerlerini Bulma
x'in alabileceği en büyük iki farklı tam sayı değeri 4 ve 3’tür (çünkü x < 5). Bu tam sayıların toplamı:
$$ 4 + 3 = 7 $$
Bu nedenle, sorunun doğru cevabı A) 7’dir.