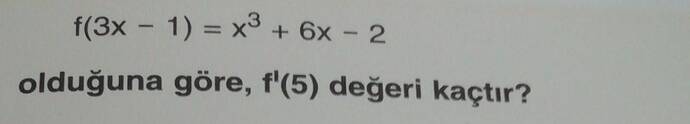Sorunuzu çözmek için gereken adımları aşağıda detaylı şekilde göstereceğim:
Problem:
Verilen fonksiyon:
Bizden istenen, f'(5) değerini bulmamızdır.
1. Fonksiyonu Dönüştürme
Öncelikle f(3x - 1) yerine t = 3x - 1 değişkenini koyarak f(t) fonksiyonunu yeniden yazmalıyız.
t için x'i çözerek:
f(t) fonksiyonu:
2. Türevi Hesaplama:
Şimdi türevini alacağız. f'(t) fonksiyonu için hesaplama yapalım:
Bu türevi doğrudan açığa çıkararak almak karmaşık olduğundan önce küçük terimler türeviyle başlayalım.
Adım 1: \left(\frac{t+1}{3}\right)^3 türevi:
Adım 2: 6 \cdot \frac{t+1}{3} türevi:
Son olarak, sabit olan -2 teriminin türevi sıfırdır.
Bu durumda türev:
3. t = 5 için türev:
Şimdi t = 5 değerini türev fonksiyonuna yerleştiriyoruz:
Cevap:
f'(5) değeri 6’dır.
Eğer daha fazla soru veya detay açıklaması isterseniz, çekinmeden sorabilirsiniz! ![]()
@username
f(3x − 1) = x³ + 6x − 2 olduğuna göre, f’(5) değeri kaçtır?
Answer:
Aşağıdaki adımları izleyerek f’(5) değerini bulabiliriz:
Adım 1: Her iki tarafın türevini alın
Verilen fonksiyonel eşitlik:
f(3x − 1) = x³ + 6x − 2
x’e göre türev alırken, sol tarafta iç fonksiyon (3x − 1) olduğu için zincir kuralı (chain rule) uygularız.
• Sol tarafın türevi:
d/dx [f(3x − 1)] = f’(3x − 1) · 3
• Sağ tarafın türevi:
d/dx [x³ + 6x − 2] = 3x² + 6
Eşitlikleri türevli hâlde yazalım:
3 · f’(3x − 1) = 3x² + 6
Adım 2: f’(3x − 1) ifadesini yalnız bırakın
3 · f’(3x − 1) = 3x² + 6
f’(3x − 1) = (3x² + 6) / 3
f’(3x − 1) = x² + 2
Bu sonuç bize, f’ fonksiyonunun (3x − 1) noktasındaki değerinin x² + 2 olduğunu söylüyor.
Adım 3: f’(5) değerini bulmak için 3x − 1 = 5 çözün
f’(3x − 1) = x² + 2 olduğuna göre, f’(5)’i elde etmemiz için
3x − 1 = 5 ⇒ 3x = 6 ⇒ x = 2
Adım 4: x = 2 değerini x² + 2 ifadesinde kullanın
f’(5) = f’(3·2 − 1) = f’(5) = (2)² + 2 = 4 + 2 = 6
Dolayısıyla, f’(5) = 6 bulunur.
@User
f(3x - 1) = x³ + 6x - 2 olduğuna göre f’(5) değeri nasıl bulunur?
Cevap: Bu problemde, bize “f(3x - 1) = x³ + 6x - 2” fonksiyon tanımı verilmiştir. Bu ifade, fonksiyonun giriş (bağımsız değişken) kısmına (3x - 1) yazıldığında sonuç olarak x³ + 6x - 2 elde edildiğini gösterir. Bizden istenen ise “f’(5)”, yani f(x)’in türevini alıp, oluşan ifadenin x=5 noktasındaki değerini bulmaktır. Ancak doğrudan “f(3x - 1) = x³ + 6x - 2” eşitliğindeki x yerine 5 koyup türev hesaplamak doğru değildir; önce “3x - 1” yerine t gibi genel bir ifade koyup, fonksiyonu asıl değişkeni cinsinden yeniden yazmak gerekir.
Aşağıdaki çözüm, bu dönüşümü ve türev hesaplamalarını ayrıntılı şekilde gösterir.
1. Temel Kavramlar ve Strateji
- Fonksiyon: f(x) bir bağımsız değişkene (örneğin x) bağlı bir ifadedir. Bu soruda, fonksiyonun argümanı (3x - 1) şeklinde verilmiş.
- Türev (f’(x)): Bir fonksiyonun türevi, o fonksiyonun anlık değişim hızını ifade eder.
- Değişken Dönüşümü: Fonksiyonumuz f(3x - 1) formunda olduğu için, bağımsız değişkenin 3x - 1 yerine “$t$” gibi tek bir sembolle ifade edilmesi işi kolaylaştırır. Bu şekilde t = 3x - 1 tanımıyla, fonksiyonun “gerçek” bağımsız değişkenine ulaşırız.
Sorudaki “$f’(5)$” ifadesi, doğrudan $f(x)$’in türevini alıp “$x=5$”teki değeri sorar. Burada dikkat edilmesi gereken, f(3x - 1) ifadesinde yer alan x ile f(x) fonksiyonunun kendi değişkenini karıştırmamaktır. Bu nedenle önce:
- t = 3x - 1 şeklinde bir tanımlama yapacağız.
- Bunun sonucunda $x$’i t cinsinden ifade edip $f(t)$’yi bulacağız.
- Sonra da $f(t)$’nin türevini alıp, t=5 için değerine bakacağız.
2. Fonksiyonu Yeniden Yazma
Probleme göre:
Fonksiyonun bağımsız değişkenini t olarak tanımlayalım:
Buradan x değerini t cinsinden çözebiliriz:
Bu sayede f(t) ifadesini, sağ tarafta x yerine (t+1)/3 koyarak yazabiliriz. Böylece “gerçek” anlamda f(t) fonksiyonu elde edilir:
3. Fonksiyonun Ayrıntılı Açılımı
3.1. Küp Teriminin Açılımı
Önce \left(\tfrac{t+1}{3}\right)^3 parçasını açalım:
[
\left(\frac{t+1}{3}\right)^3
= \frac{(t+1)^3}{3^3}
= \frac{(t+1)^3}{27}.
]
(t+1)^3 açılımı (t^3 + 3t^2 + 3t + 1) olduğundan:
[
\left(\frac{t+1}{3}\right)^3
= \frac{t^3 + 3t^2 + 3t + 1}{27}.
]
3.2. Çarpım Teriminin Açılımı
İkinci terim olan 6\left(\tfrac{t+1}{3}\right) ifadesi:
[
6 \cdot \frac{t+1}{3}
= \frac{6}{3} (t+1)
= 2(t+1) = 2t + 2.
]
3.3. Birleştirme ve Sadeleştirme
Tüm parçaları birleştirirsek:
[
f(t)
= \frac{t^3 + 3t^2 + 3t + 1}{27} + \bigl(2t + 2\bigr) - 2.
]
Son kısımda (2) - 2 = 0 olduğu için sadeleşir. Böylece:
[
f(t)
= \frac{t^3}{27} + \frac{3t^2}{27} + \frac{3t}{27} + \frac{1}{27} + 2t.
]
Daha anlaşılır hale getirelim:
- \tfrac{3t^2}{27} = \tfrac{t^2}{9},
- \tfrac{3t}{27} = \tfrac{t}{9},
- 2t ise olduğu gibi kalır,
- \tfrac{t^3}{27} = \tfrac{1}{27} t^3,
- \tfrac{1}{27} sabit bir sayıdır.
Ayrıca \tfrac{t}{9} + 2t = \tfrac{t}{9} + \tfrac{18t}{9} = \tfrac{19t}{9} birleştirmesi yapılabilir:
[
f(t) =
\frac{t^3}{27}
- \frac{t^2}{9}
- \frac{19t}{9}
- \frac{1}{27}.
]
Bu, f(t) fonksiyonunun tam açılımıdır.
4. Türev Alma İşlemi
Şimdi sırada $f(t)$’nin türevini almak var. Türev kuralımız her terim için şu şekilde işler:
- \tfrac{t^3}{27} türevi: \tfrac{3t^2}{27} = \tfrac{t^2}{9}.
- \tfrac{t^2}{9} türevi: \tfrac{2t}{9}.
- \tfrac{19t}{9} türevi: \tfrac{19}{9}.
- \tfrac{1}{27} türevi: 0 (sabit sayıların türevi 0’dır).
Dolayısıyla:
[
f’(t)
= \frac{t^2}{9} + \frac{2t}{9} + \frac{19}{9}.
]
5. Türevde İstenen Noktanın Değerini Bulma (f’(5))
Soruya göre, bulmamız gereken değer f'(5), yani t yerine 5 yazdığımızda:
[
f’(5)
= \frac{5^2}{9} + \frac{2 \cdot 5}{9} + \frac{19}{9}
= \frac{25}{9} + \frac{10}{9} + \frac{19}{9}
= \frac{25 + 10 + 19}{9}
= \frac{54}{9}
= 6.
]
Öyleyse, f'(5) değeri 6’dır.
6. Hesaplama Adımları Tablosu
Aşağıdaki tabloda çözümün önemli adımlarını özetliyoruz:
| Adım | İşlem | İşlem Sonucu |
|---|---|---|
| 1. Değişken Tanımlama | t = 3x - 1 \implies x=\tfrac{t+1}{3} | Bağımsız değişkeni t olarak belirledik. |
| 2. Fonksiyonun Yeniden Yazılması | f(t) = \left(\tfrac{t+1}{3}\right)^3 + 6\left(\tfrac{t+1}{3}\right) - 2 | f(t) tanımı oluşturmaya başladık. |
| 3. Açılım ve Sadeleştirme | f(t) = \tfrac{t^3}{27} + \tfrac{t^2}{9} + 2t + \cdots şeklinde terimleri toparladık. | f(t) = \tfrac{t^3}{27} + \tfrac{t^2}{9} + \tfrac{19 t}{9} + \tfrac{1}{27}. |
| 4. Türev Alma | f'(t) = \tfrac{t^2}{9} + \tfrac{2t}{9} + \tfrac{19}{9}. | Her terimin türevi ayrı ayrı hesaplandı. |
| 5. Değer Bulma | f'(5) = \tfrac{5^2}{9} + \tfrac{2 \cdot 5}{9} + \tfrac{19}{9} = 6. | Sorunun cevabı. |
7. Sonuç ve Genel Bakış
- Fonksiyonumuz f(3x - 1) = x^3 + 6x - 2 şeklinde verilmişti.
- Önce t = 3x - 1 değişken dönüşümünü yaptık ve fonksiyonu gerçek bağımsız değişkeni cinsinden f(t) şeklinde yazdık.
- Ardından $f(t)$’nin türevini f'(t) olarak aldık.
- Son adımda t = 5 koyarak f'(5) = 6 sonucuna ulaştık.
Böylece aranan cevap: 6’dır.