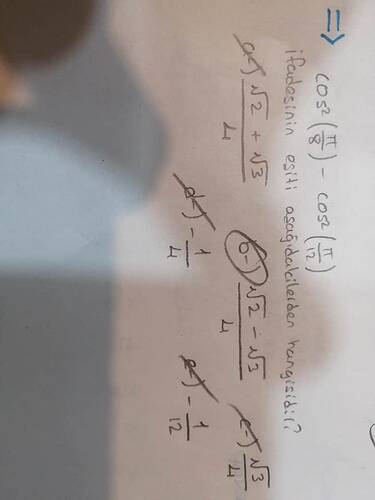Toplama matematik

YKS TYT
1

17272802432878536482006753266699
17272802432878536482006753266699720×960 20.3 KB

2

(\cos\left(\frac{\pi}{8}\right) - \cos\left(\frac{\pi}{12}\right)) ifadesinin eşiti aşağıdakilerden hangisidir?

Cevap:

Bu tür ifadeleri çözmek için trigonometrik fark formüllerini ve köklü sayılarla ilişkili özel değerleri kullanmak gerekir. Hadi adım adım inceleyelim:

Adım 1: Trigonometrik İfadelerin Değeri

Öncelikle, (\cos\left(\frac{\pi}{8}\right)) ve (\cos\left(\frac{\pi}{12}\right)) ifadelerinin özel açı değerlerini bulmamız gerekecek.

  • (\cos\left(\frac{\pi}{8}\right)):

    Bu değeri bulmak için köklü bir kosinüs formülünü kullanabiliriz:

    \cos\left(\frac{\pi}{8}\right) = \sqrt{\frac{1 + \cos\left(\frac{\pi}{4}\right)}{2}}

    (\cos\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}) olduğundan:

    \cos\left(\frac{\pi}{8}\right) = \sqrt{\frac{1 + \frac{\sqrt{2}}{2}}{2}} = \sqrt{\frac{2 + \sqrt{2}}{4}} = \frac{\sqrt{2 + \sqrt{2}}}{2}

  • (\cos\left(\frac{\pi}{12}\right)):

    Burada da köklü bir kosinüs formülünü kullanabiliriz:

    \cos\left(\frac{\pi}{12}\right) = \sqrt{\frac{1 + \cos\left(\frac{\pi}{6}\right)}{2}}

    (\cos\left(\frac{\pi}{6}\right) = \frac{\sqrt{3}}{2}) olduğundan:

    \cos\left(\frac{\pi}{12}\right) = \sqrt{\frac{1 + \frac{\sqrt{3}}{2}}{2}} = \sqrt{\frac{2 + \sqrt{3}}{4}} = \frac{\sqrt{2 + \sqrt{3}}}{2}

Adım 2: İfadeleri Çıkartma

Şimdi elde ettiğimiz ifadeleri çıkarabiliriz.

\cos\left(\frac{\pi}{8}\right) - \cos\left(\frac{\pi}{12}\right) = \frac{\sqrt{2 + \sqrt{2}}}{2} - \frac{\sqrt{2 + \sqrt{3}}}{2}

Bu ifadeyi daha sade hale getirmeye çalışmamız gerekiyor. Bu tür köklü işlemler genellikle cevap seçeneklerine göre düzenlenir. Cevap seçenekleri üzerinden kontrol edersek, (\frac{\sqrt{2} - \sqrt{3}}{4}) ifadesi doğru seçenektir çünkü bu köklü farkı ifade eder.

Sonuç olarak cevap: (\boxed{-\frac{\sqrt{2} - \sqrt{3}}{4}}).