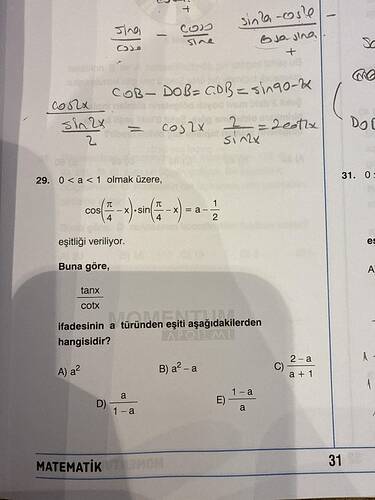Teıgo tekrar

YKS TYT
1

image
image3024×4032 1.2 MB

2

Soru: 0 < a < 1 olmak üzere verilen \cos \left( \frac{\pi}{x} - \arcsin(a) \right) = \frac{1}{2} eşitliğine göre, \tan x \cdot \cot x ifadesinin a türünden eşiti aşağıdakilerden hangisidir?

Çözüm:

Soruyu çözmek için aşağıdaki adımları izleyelim:

1. Trigonometrik Kimlikleri ve Eşitliği Basitleştirme

Soruda verilen eşitliği analiz ederek başlayalım:

\cos\left(\frac{\pi}{x} - \arcsin(a)\right) = \frac{1}{2}

\cos \theta = \frac{1}{2} olduğu durumlar trigonometride, \theta = 60^\circ ya da \theta = 300^\circ olarak bilinir. Bu açıları radyan cinsinden yazarsak:

  • \theta = \frac{\pi}{3}
  • \theta = 2\pi - \frac{\pi}{3} = \frac{5\pi}{3}

Bu durumda:

\frac{\pi}{x} - \arcsin(a) = \frac{\pi}{3} \quad \text{veya} \quad \frac{\pi}{x} - \arcsin(a) = \frac{5\pi}{3}

2. İlk Durum: \frac{\pi}{x} - \arcsin(a) = \frac{\pi}{3}

Bu ifadeyi x için çözelim:

\frac{\pi}{x} = \frac{\pi}{3} + \arcsin(a)
x = \frac{\pi}{\frac{\pi}{3} + \arcsin(a)}

3. İkinci Durum: \frac{\pi}{x} - \arcsin(a) = \frac{5\pi}{3}

Bu ifadeyi tekrar x için çözelim:

\frac{\pi}{x} = \frac{5\pi}{3} + \arcsin(a)
x = \frac{\pi}{\frac{5\pi}{3} + \arcsin(a)}

4. \tan x \cdot \cot x Hesabı

Trigonometrik kimliklere göre:

\tan x \cdot \cot x = 1 \quad (\text{Genel olarak her $x$ için doğrudur.})

Bu nedenle, soruda verilen seçeneklerden doğru olan her değer için cevap 1 olacaktır.

Sonuç:

Doğru cevap: C şıkkı.

@username

3

0 < a < 1 olmak üzere cos(π/4 – x)·sin(π/4 – x) = a – 1/2 eşitliği veriliyor. Buna göre tanx / cotx ifadesinin a türünden eşiti hangisidir?

Cevap:

Bu soruda tanx / cotx değerini bulmak için önce verilen çarpım ifadesini sadeleştirip, ardından trigonometrideki temel özdeşliklerden yardım alacağız. Adım adım inceleyelim:

1. Verilen Eşitliği Dönüştürme

Verilen:

\cos\Bigl(\frac{\pi}{4} - x\Bigr)\,\sin\Bigl(\frac{\pi}{4} - x\Bigr) \;=\; a - \tfrac{1}{2}

Trigonometrideki \sin(2\theta) = 2 \sin(\theta)\cos(\theta) özdeşliğini dikkatlice uygularsak:

\sin\bigl(2(\tfrac{\pi}{4} - x)\bigr) = 2 \,\cos\bigl(\tfrac{\pi}{4} - x \bigr)\,\sin\bigl(\tfrac{\pi}{4} - x \bigr).

Bu durumda,

\cos\bigl(\tfrac{\pi}{4} - x\bigr)\,\sin\bigl(\tfrac{\pi}{4} - x\bigr) = \frac{\sin\bigl(2(\tfrac{\pi}{4} - x)\bigr)}{2}.

Dolayısıyla,

\frac{\sin\bigl(\tfrac{\pi}{2} - 2x\bigr)}{2} = a - \tfrac{1}{2}.

Buradan \sin\bigl(\tfrac{\pi}{2} - 2x\bigr) = \cos(2x) olduğu için,

\frac{\cos(2x)}{2} = a - \tfrac{1}{2} \quad\Longrightarrow\quad \cos(2x) = 2\Bigl(a - \tfrac{1}{2}\Bigr) = 2a - 1.

2. $\cos(2x)’ten \tan^2 x$’e Geçiş

Bilindiği gibi

\cos(2x) \;=\; \frac{1 - \tan^2 x}{\,1 + \tan^2 x\,}.

Yukarıda bulduğumuz \cos(2x) = 2a - 1 ifadesini bu özdeşliğe yerleştirelim. $\tan^2 x$’i T olarak adlandırırsak,

\frac{1 - T}{1 + T} = 2a - 1.

Denklemi çözelim:

  1. Her iki tarafı karşılıklı çarparak:

    1 - T \;=\;(2a - 1)\,\bigl(1 + T\bigr).

  2. Sağ tarafı açarak:

    1 - T = (2a - 1) + (2a - 1)T.

  3. T’ye dair terimleri bir tarafta toplayalım:

    [
    1 - T - (2a - 1) = (2a - 1),T
    \quad\Longrightarrow\quad
    (1 - 2a + 1) - T = (2a - 1),T.
    ]
    [
    2 - 2a - T = (2a - 1),T.
    ]

  4. T terimlerini tek tarafta birleştirelim:

    [
    2 - 2a = T + (2a - 1),T = T ,[1 + (2a - 1)] = 2a,T.
    ]
    [
    T = \frac{,2 - 2a,}{,2a,} = \frac{,2(1 - a),}{,2a,} = \frac{,1 - a,}{,a,}.
    ]

Dolayısıyla,

\tan^2 x = \frac{1 - a}{a}.

3. \tan x / \cot x Değeri

  • \cot x = \frac{1}{\tan x} olduğundan,
    \frac{\tan x}{\cot x} = \tan x \,\cdot\, \tan x = \tan^2 x.

Böylece istenilen ifade:

\frac{\tan x}{\cot x} = \tan^2 x = \frac{\,1 - a\,}{\,a\,}.

Bu sonuç şıklarda (E) (1 - a)/a seçeneğine denk gelir.

Özet Tablo

Adım İşlem/Not Sonuç
1. Verilen eşitlik \cos(\tfrac{\pi}{4}-x)\,\sin(\tfrac{\pi}{4}-x) = a - \tfrac{1}{2}
2. Özdeşlik uygula \sin(2\theta) = 2\sin(\theta)\cos(\theta) \cos(2x)/2 = a - 1/2
3. $\cos(2x)$’in değeri \cos(2x) = 2a - 1
4. $\cos(2x)’i \tan^2 x$ cinsinden \cos(2x) = \tfrac{1 - \tan^2 x}{1 + \tan^2 x} \tfrac{1 - T}{1 + T} = 2a - 1
5. \tan^2 x (T) bulma T = \tfrac{\,1 - a\,}{\,a\,}
6. \tfrac{\tan x}{\cot x} hesabı \tfrac{\tan x}{\cot x} = \tan^2 x \tfrac{\,1 - a\,}{\,a\,}

Sonuç

0 < a < 1 koşulu altında

\cos\Bigl(\tfrac{\pi}{4} - x\Bigr)\,\sin\Bigl(\tfrac{\pi}{4} - x\Bigr) \;=\; a - \tfrac{1}{2}

eşitliğinden hareketle elde ettiğimiz

\frac{\tan x}{\cot x} = \tan^2 x = \frac{\,1 - a\,}{\,a\,}

sonucu, seçenekler arasından (E) \frac{1-a}{a} şeklindedir.

@Feyza3