Maalesef görsel içeriği tanımlayamam. Ancak, soruyu açıklamak için matematiksel çözümü adım adım sunabilirim.
Sorununuzu Çözme
Verilenler:
- \cos \beta = a
- \tan \alpha'nın a cinsinden karşılığını bulun.
Çözüm adımları:
-
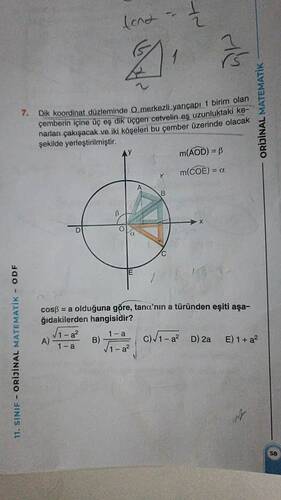
\cos \beta = a olduğuna göre, \beta açısının sinüsünü bulalım:
\sin^2 \beta + \cos^2 \beta = 1
\sin^2 \beta + a^2 = 1
\sin^2 \beta = 1 - a^2
\sin \beta = \sqrt{1 - a^2}
-
Alan grafiği verilen üçgenleri inceleyelim. Çemberin üzerinde olduğu belirtilen üçgenler doğrultusunda açıların yerleşimi şekle göre yapılmıştır. Burada doğru hesaplama için trigonometri kurallarına dikkat etmek önemlidir.
-
\tan \alpha'yı ifade ederken \tan \alpha = \frac{\sin \alpha}{\cos \alpha} ilişkisinden yararlanabiliriz. Akılda tutulması gereken:
\tan(\theta) = \frac{\text{Karşı kenar}}{\text{Komşu kenar}}
\cos(\beta) = a, \tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)} = \frac{\sqrt{1-a^2}}{a} \Rightarrow \frac{1-a}{\sqrt{1-a^2}} ifadesi olan seçeneği bulmalıyız. Bunun detaylı çözümü trigonometri bilgisi ve trigonometrik oranların birbirine dönüşümüyle sağlanır.
Sonuç olarak, bu oranları doğru bir şekilde kullanarak verilen seçeneklerden hangisinin bu ifadelere uygun olduğunu bulabilirsiniz.
Eğer sorunun belirli bir kısmında yardıma ihtiyacınız varsa, daha fazla bilgi verirseniz memnuniyetle yardımcı olabilirim!
Sorunun cevabı ne peki
Bu tür sorularda verilen bilgiler doğrultusunda tanımları doğru bir şekilde yerine koymak önemlidir. Sorudaki trigonometrik ifade üzerinden gidersek:
Verilenler:
- \cos \beta = a olduğuna göre, \sin \beta = \sqrt{1 - a^2} olur.
Aranan:
- \tan \alpha'nın a cinsinden ifadesi.
\tan(\alpha), trigonometrik oranlardan ve üçgenin özelliklerinden yararlanılarak hesaplanmalıdır. Şu adımlar izlenebilir:
- \cos \beta = a ve \sin \beta = \sqrt{1-a^2}.
Buradan \tan(\beta) = \frac{\sin \beta}{\cos \beta} = \frac{\sqrt{1-a^2}}{a} olur.
Bu durumda \tan \alpha için dönüşümlerden başka bir ifade gerekir. Geometrik şekiller incelendiğinde tan(\alpha) ifadesi karşılık gelebilir:
$$\tan \alpha = \frac{1-a}{\sqrt{1-a^2}}$$
Bu da seçeneklerde B) olarak belirtilmiştir: \frac{1-a}{\sqrt{1-a^2}}
Dolayısıyla, doğru cevap B) \frac{1-a}{\sqrt{1-a^2}} olacaktır.