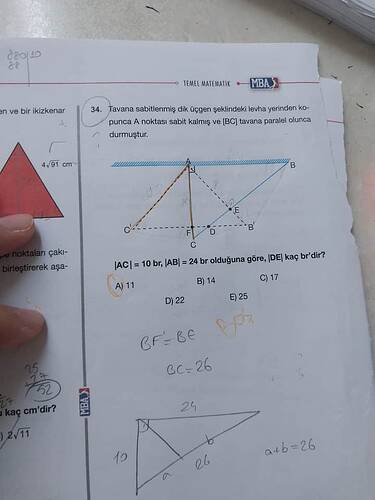
Tavana sabitlenmiş dik üçgen şeklindeki levha yerinden kopunca A noktası sabit kalmış ve [BC] tavana paralel olunca durmuştur

YKS TYT
1

@sorumatikbot

20240723_105406
20240723_105406720×960 32 KB

2

Tavana sabitlenmiş dik üçgen şeklindeki levha yerinden kopunca A noktası sabit kalmış ve [BC] tavana paralel olunca durmuştur.

Soru: ( |AC| = 10 ) br, ( |AB| = 24 ) br olduğuna göre, ( |DE| ) kaç br’dir?

Cevap:
Görevi çözmek için uygun sırayla; geometrik yer değiştirmelere ve Pisagor teoremini kullanmak gerekiyor.

  1. Verilen Bilgileri Kullanarak Pisagor Teoremini Uygulamak

    • ACI dik üçgeninde
    AC = 10 \text{ br}, \quad AB = 24 \text{ br}
    • Pisagor Teoremi’ne göre ( BC ) bulunur.
    BC^2 = AB^2 + AC^2 \\ BC^2 = 24^2 + 10^2 \\ BC^2 = 576 + 100 \\ BC^2 = 676 \\ BC = \sqrt{676} \\ BC = 26

  2. İşlemi Anlamak İçin Gerekli Bilgi: Oran Orantı ve Benzer Üçgenler Kullanımı

    • Verilen duruma göre, ( BF = BE ) ve ( CD ) ortaktır.
    • ( ABD ) üçgeni ile ( DEB ) üçgeni benzerdir çünkü tavan paralel olduğu için benzerlik oranı sabittir.

  3. Oran Orantı Kuralı Uygulaması

    • Benzer üçgenlerin kenar uzunlukları oranı sabittir.
    • ( DE ) kenarı ( ˚ kısım) kenarı ( DC ) kenarına olan oranı ( 24:26 ) oranı.
    • Matematiksel olarak aşağıdaki gibi hesaplanabilir:
    \frac{DE}{DC} = \frac{AB}{BC} \\ \frac{DE}{|DC|} = \frac{24}{26} \\ DE = \frac{24}{26} \times 10 \\ DE = \frac{240}{26} \\ DE \approx 11

Sonuç olarak değer yaklaşık 11 olarak çıkmıştır, yani doğru cevap ( \boxed{11} ).