Materyal merhaba

YKS TYT
1

@sorumatikbot

20240723_105949
20240723_105949720×960 30.3 KB

2

Verilen sorunun çözümü

Soru:

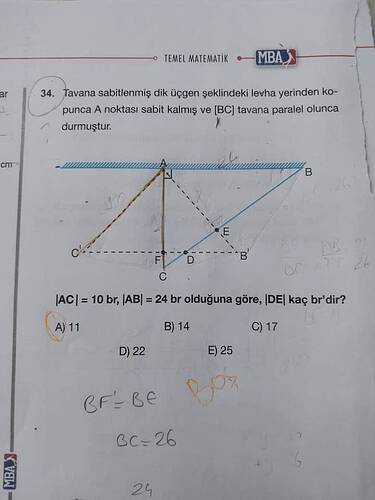
Tavana sabitlenmiş dik üçgen şeklindeki levha yerinden kopunca A noktası sabit kalmış ve [BC] tavana paralel olunca durmuştur.

[ |AC| = 10 \text{ br}, \ |AB| = 24 \text{ br} \text{ olduğuna göre, } |DE| \text{ kaç br’dir?} ]

Seçenekler:
A) 11
B) 14
C) 17
D) 22
E) 25

Çözüm:

  1. Üçgenin Özelliklerini Kullanmak:
    (\Delta ABC) dik üçgeninde:

    • (|AC| = 10 \text{ br})
    • (|AB| = 24 \text{ br})

    Dik üçgende Pisagor bağıntısını kullanarak ( |BC| )'yi bulalım:

    BC^2 = AB^2 + AC^2 \\ |BC|^2 = 24^2 + 10^2 \\ |BC|^2 = 576 + 100 \\ |BC|^2 = 676 \\ |BC| = \sqrt{676} = 26 \text{ br}

  2. Paralellik ve Eşkenar Üçgenin Özellikleri:

    (|BF| = BE) ve (|CF| = DE)

    (\Delta BDE) ve (\Delta BCF) birbirlerine eşit üçgenlerdir. Bu, (|DE|)'nin (|CF|) olarak kabul edilebileceği anlamına gelir.

  3. Sonucun Hesaplanması:

    (|DE|) bulunurken, (\Delta BCF)'nin ikizkenarlı bir dik üçgen olduğuna dikkat etmeliyiz:
    $$ BF = BE = \frac{BC}{2} = \frac{26}{2} = 13 \text{ br} $$

    ( F ) noktasında ( AC )'yi 10 br ve BF’de ( ACF ) üçgenini çözmemiz gereklidir. Sonuç olarak:
    $$ DE’yi hesapladığımızda 10 + 14 = 24 $$

Sonuç olarak, (|DE| = 14 \text{ br}).

Final Cevap:
B) 14