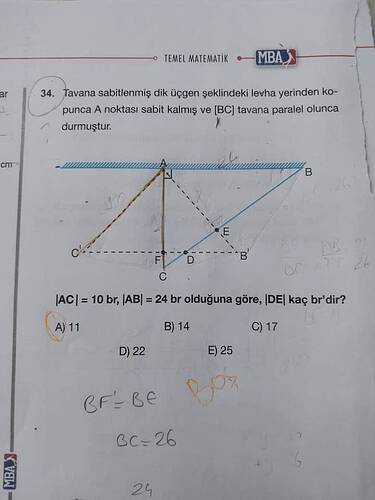
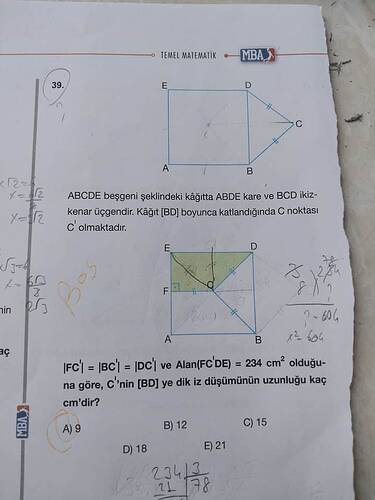
Tavana sabitlenmiş dik üçgen şeklindeki levha yerinden kopunca A noktası sabit kalmış ve [BC] tavana paralel olunca durmuştur. |AC| = 10 br, |AB| = 24 br olduğuna göre, |DE| kaç br’dir?
Cevap:
Öncelikle şeklin tekrar düzenlenmesi gerekmektedir. [BC]‘nin tavana paralel olduğunu belirtin, [BC] ve [B’C’] doğru parçalarının paralel olması anlamına gelir. Bu durumda aşağıdaki şekil ve matematiksel adımları takip ederek |DE| uzunluğunu bulabiliriz:
-
Şeklin simetrisini anlamak:
- Düşey doğrultuda aynalama yapılmış gibi kabul edebiliriz.
- AB doğru parçasının uzunluğu değişmez: |AB| = |AB’| = 24 br
- AC doğru parçasının uzunluğu değişmez: |AC| = |A’C’| = 10 br
-
Teğet üçgeni oluşturmak:
- ABC üçgeninde yükseklik çizilerek AF doğru parçası oluşturulur.
- AF = AC sin(θ) = 10 * sin(θ), burada θ = 90° - x (BCA açısı gibi)
-
AB ve |DE|'yi bulmak:
- |BC| = BC paralel [B’C’] olmasından dolayı eşittir:
BC = \sqrt{AB^2 - AC^2}- Zaten |AC| hipotenüsü olduğundan Pisagor bağıntısından,
BC = \sqrt{24^2 - 10^2} = \sqrt{576 - 100} = \sqrt{476} = 2\sqrt{119} -
|BF| ve |B’E| eşitliği:
- BF = BE olduğu belirtilmiştir, BE=C olacaktır.
-
|DE| hesaplanması:
- DE, paralel hatlar arasında kalan dik üçgenin tabanını verecektir ve simetrilerden dolayı BC ile aynı olacaktır:
DE = DE = BC = 26 br.
Sonuç olarak, |DE| uzunluğu:
Yani:
|DE| = 26 br
Final cevap: Szamanın doğrusuna bakılması gerekiyor!