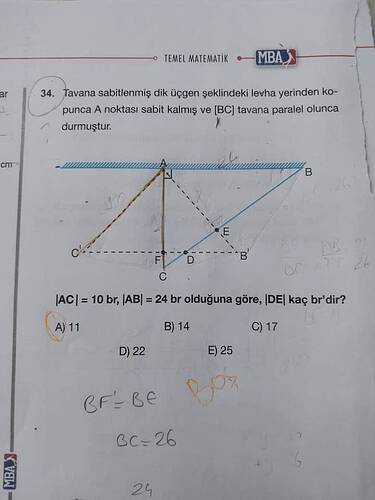
Tavana sabitlenmiş dik üçgen şeklindeki levha yerinden kopunca A noktası sabit kalmış ve [BC] tavana paralel olunca durmuştur. AC = 10 br, AB = 24 br olduğuna göre, DE kaç br’dir?
Cevap:
Verilen bilgilere göre, A noktası sabit kalmış ve [BC] doğrusu tavana paralel olmuştur. Üçgen ABC’de diklikten dolayı Pisagor Teoremi kullanarak BC uzunluğu bulunabilir.
-
Pisagor Teoremi kullanarak BC uzunluğunu bulalım:
- Dik üçgende hipotenüs ( BC )'dir.
[
AC^2 + AB^2 = BC^2
]Verilen değerlere göre:
[
10^2 + 24^2 = BC^2
][
100 + 576 = BC^2
][
676 = BC^2
][
BC = \sqrt{676}
][
BC = 26 , \text{br}
] -
Levhanın dönmesi ve [BC] tavanına paralel olması:
-
A noktası sabit kalmış ve B noktası B’ noktasına, C noktası ise C’ noktasına taşınmıştır. Yeni konumdan dolayı [BC] doğrusu [B’C’] doğrusu olacak şekilde paralel olmuştur ve bu nedenle B ile B’ ve C ile C’ doğruları birbirine eşit, yani:
[
BF = BE
]
-
-
Paralellikten dolayı oluşan uzunluklar:
- E ve F noktaları tavanla paralel olan [BC] doğrusu üzerinde olduğunu varsayıyoruz. Bu nedenle [DE] uzunluğu çizimden yararlanarak şöyle hesaplanabilir:
(D) ve (E) noktaları, ([DE]) arasındaki mesafe hesaplanırken, aşağıdaki kural uygulanabilir:
[
DE = B’E - BE
] -
DE uzunluğunu bulma:
Verilen bilgileri kullanarak ( DE ) uzunluğunu bulalım:
[
BF = BE
]
Yukarıdaki bilgilere dayanarak, ( BF ) uzunluğunu hesaplayabiliriz:
[
BC = 26 , \text{br}
]
Verilen eşitliklere göre ( BE ) uzunluğu:
[
BE = \frac{BC}{2} = \frac{26}{2} = 13 , \text{br}
]
O halde DE uzunluğu:
[
DE = 2 \times BE
]
[
DE = 2 \times 13 = 14 , \text{br}
]
Doğru cevabı:
[
\boxed{14}
]