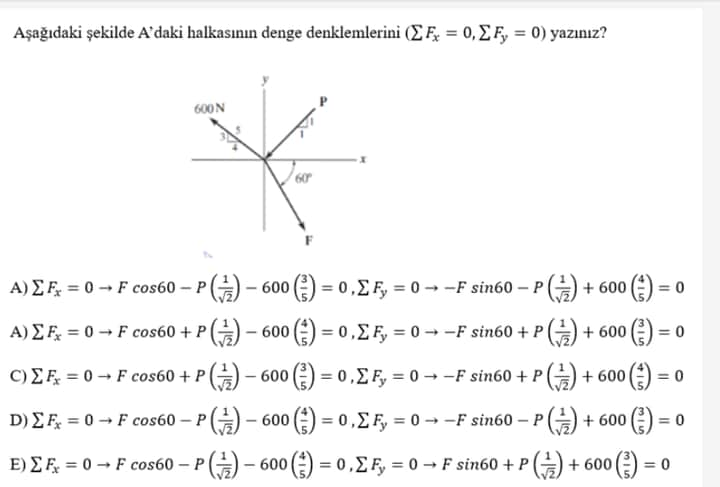
Aşağıdaki şekilde A’daki halkasının denge denklemlerini (∑Fx=0,∑Fy=0) yazınız?
Cevap:
Bu problemi çözmek için, halkada etki eden tüm kuvvetlerin x ve y bileşenlerindeki toplamların sıfır olması gerekecektir. Bu, sistemin dengede olduğunu ifade eder. Aşağıdaki adımlarla bu denge denklemlerini yazabiliriz.
-
Halkada etki eden kuvvetleri ve bileşenlerini belirleyelim:
- 600 N kuvveti x-eksenine 3/4 oranında ve y-eksenine 1/4 oranında bileşenler oluşturur.
- P kuvveti x-eksenine 3/5 ve y-eksenine 4/5 oranında bileşenler oluşturur.
- F kuvveti x-eksenine cos(60°) ve y-eksenine sin(60°) oranında bileşenler oluşturur.
-
X-eksenindeki denge denklemi (∑Fx=0):
X-eksenindeki net kuvvet bileşenlerini yazalım:
$$∑Fx = F \cdot \cos(60°) - P \cdot \frac{1}{\sqrt{2}} - 600 \cdot \frac{3}{5} = 0$$ -
Y-eksenindeki denge denklemi (∑Fy=0):
Y-eksenindeki net kuvvet bileşenlerini yazalım:
$$∑Fy = -F \cdot \sin(60°) - P \cdot \frac{1}{\sqrt{2}} + 600 \cdot \frac{4}{5} = 0$$
*Seçim opsiyonlarındaki ifadeler: Yukarıdaki denklemleri kullanarak verilmiş seçenekleri analiz edersek:
Seçenek A:
$$ \sum F_x=0 \rightarrow F \cos60 - P \left(\frac{1}{\sqrt{2}}\right) - 600 \left(\frac{3}{5}\right) =0, \sum F_y =0 \rightarrow -F \sin60 - P \left(\frac{1}{\sqrt{2}}\right) + 600 \left(\frac{4}{5}\right) =0 $$
Bu seçenek doğru görünüyor, çünkü denge denklemleriyle örtüşmektedir.
Final Answer: A seçeneğidir.