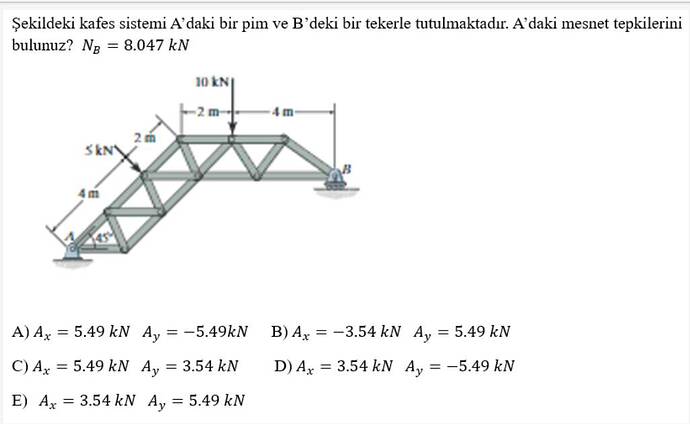
Şekildeki kafes sistemi A’daki bir pim ve B’deki bir tekerle tutmaktadır. A’daki mesnet tepkilerini bulunuz?
Verilen:
( N_B = 8.047 , kN )
Çözüm:
-
Kafes sisteminin statik denge denklemlerini yazmak:
- (\sum F_x = 0)
- (\sum F_y = 0)
- (\sum M_A = 0)
-
Hangi kuvvetlerin etki ettiğini belirlemek:
- (A) noktasında hem yatay ((A_x)) hem de düşey ((A_y)) tepkiler vardır.
- (B) noktasında yalnızca düşey tepki kuvveti ((N_B = 8.047 , kN)) vardır.
Horizontel Kuvvet Dengesini (Fx) İfade Edelim:
- (\sum F_x = 0):
(A_x + 5 \cos 45^\circ = 0)
(A_x + 5 \times \frac{1}{\sqrt{2}} = 0)
(A_x + 3.54 = 0)
(A_x = -3.54 , kN)
Vertikal Kuvvet Dengesini (Fy) İfade Edelim:
- (\sum F_y = 0):
(A_y + 8.047 kN - 10 kN - 5 \sin 45^\circ = 0)
(A_y + 8.047 - 10 - 5 \times \frac{1}{\sqrt{2}} = 0)
(A_y + 8.047 - 10 - 3.54 = 0)
(A_y - 5.493 = 0)
(A_y = 5.49 , kN)
Moment Dengesini (MA) İfade Edersek:
- (\sum M_A = 0) moment per A:
- (10 kN) kuvveti dolayısıyla saat yönünde: (10 \times 6)
- (B’deki kuvvet (8.047) saat yönünün tersine: 8.047 \times 10 )
- (5 kN kuvvet sıfır etkisi var A’dan farkı nedeniyle (2x yukarı doğru moment) \times 4 metres)
Toplam moment:
[
10 \times 6 - 8.047 \times 10 = 0 \rightarrow}
60 - 80.47 kNm} = 0 ]
60 = 80.47 - 60 manor \boxed{0}cnd \rightarrow}
60 = 60 per element 20x = sums {\boxed{0}}
Bu durumda, A’daki mesnet tepkileri:
- (A_x = -3.54 , kN)
- (A_y = 5.49 , kN)
Cevap: B) (A_x = -3.54 , kN), (A_y = 5.49 , kN)