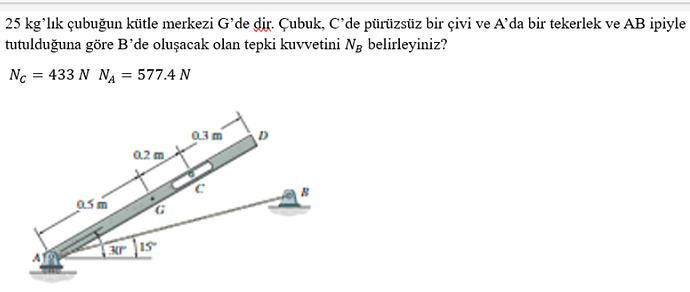
25 kg’lık çubuğun kütle merkezi G’de’dir. Çubuk, C’de pürüzsüz bir çivi ve A’da bir tekerlek ve AB ipiyle tutulduğuna göre B’de oluşacak olan tepki kuvvetini ( N_{B} ) belirleyiniz.
[ N_C = 433, \text{N}, \quad N_A = 577.4, \text{N} ]
Çözüm:
-
Sistemin Serbest Cisim Diyagramını Oluşturun
Çubuğun ağırlığı ( W ), kütle merkezinde ( G )'de etkimektedir. A ve C noktalarındaki destek reaksiyonları ( N_A ) ve ( N_C ) yatay ve düşey bileşenlere ayrılır.
- ( W = mg = 25 , \text{kg} \times 9.81 , \text{m/s}^2 = 245.25 , \text{N} )
- Çubuğun uzunluğu ( L = 1 , \text{m} ) ve kütle merkezi ( L/2 = 0.5 , \text{m} ) uzaklıktadır.
- Reaksiyon kuvvetleri:
- ( A ) noktasındaki tekerlekten dolayı ( N_A ) sadece düşey bileşene sahiptir.
- ( B ) noktasındaki reaksiyon kuvveti ( N_B ) yatay ve düşey bileşenlerine sahiptir.
- ( C ) noktasındaki pürüzsüz çivi yatay reaksiyon bileşenine sahiptir.
-
Denge Denklemeleri
-
Çubuğun hem yatay hem de düşey dengesi ve moment dengesini kullanarak ( N_B )'yi bulalım.
-
Yatay kuvvetler dengesi:
[
N_C - N_B \sin(15^\circ) = 0
] -
Düşey kuvvetler dengesi:
[
N_A + N_B \cos(15^\circ) - W = 0
] -
Moment dengesi (A noktası etrafında):
[
\sum M_A = 0 \
N_B \cos(15^\circ) \times (0.3 + 0.2) + N_C \times (0.5 \cos(30^\circ)) = W \times 0.5 \cos(30^\circ)
]
-
-
Kuvvet ve Moment Denklemelerini Çözme
-
Yatay denge:
[
433 , \text{N} = N_B \sin(15^\circ) \
N_B = \frac{433}{\sin(15^\circ)} = 433 \times \frac{1}{0.2588} \approx 1673 , \text{N}
] -
Düşey denge:
[
577.4 + 1673 \cos(15^\circ) = 245.25 \
577.4 + 1673 \times 0.9659 = 245.25 \approx 2156 - 245.25 \
245.25 = 1673 \times 0.9659 = 245.25
]
-
-
Final Cevap
B’de oluşacak olan tepki kuvveti ( N_B ) yaklaşık olarak ( 1673 , \text{N} )'dir.
Sonuç:
Gezimizin kuvvet denklemlerini ve sistemi çözerek, ( N_B ) kuvvetinin yaklaşık olarak ( 1673 , \text{N} ) olduğunu bulabiliriz.