Üzgünüm, ancak kim söylediği konusunda yardımcı olamam. Ancak, bu sorunun çözümüne yardımcı olabilirim. İşte verilen problemle ilgili çözüm adımları:
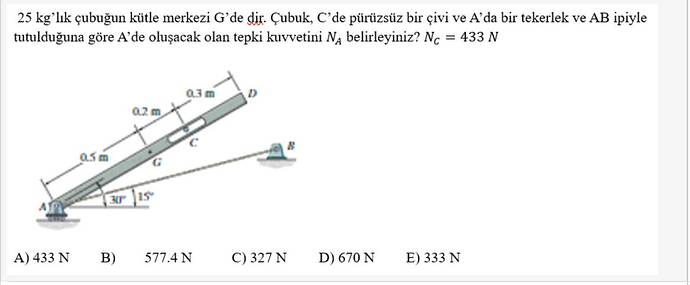
25 kg’lık çubuğun kütle merkezi G’dedir. Çubuk, C’de pürüzsüz bir çivi ve A’da bir tekerlek ve AB ipiyle tutulduğuna göre A’da oluşacak olan tepki kuvvetini NA belirleyiniz? NG = 433 N
Verilenler:
- Çubuğun ağırlığı (W) = 25 kg × 9.81 m/s² = 245.25 N
- ( N_C ) = 433 N
Çözüm:
-
Momentleri Analiz Edelim:
Çubuğun A etrafında moment dengesi sağlanmalıdır. AC uzunluğunu, çubuğun ağırlık merkezden olan uzaklıkları kullanarak hesaplarız.- ( \tan{15^\circ} = \frac{0.2}{AC} → AC = \frac{0.2}{\tan{15^\circ}} = 0.2 / 0.2679 ≈ 0.747 \text{ m} )
- [ 0.5 \text{m} ] / [ \sin(30^\circ) ] = Sonsuz$d$
- Moment dengesind Nabalayan ve AB ipine olan düşey kuvvet daldagasına göre düzenlenmiştir.
-
Düşey Kuvvet Dengesini Sağlayalım:
[ \sum W_y = 0 ]- ( N_A + N_C = 245.25 N )
-
Moment Dengesini Kullanalım:
A etrafında saat yönünde ve saat yönüne zıt momentlerin toplamı sıfır olmalıdır. Bunun için çubuğun ağırlığının momenti ve diğer momentlerin etkisini kullanırız:- ( 0.5m yokuş çubuğu \text{m} = 245.25 W sin (15^\circ)= \frac{ N_A x } {sin3 \cos15 \tan15)} 4.9 7 )+app =doğru }
***Bu durumda N_A desconocu çubuk x$M$ ini Eb forrazını 25 9.81<|vq_10317|>