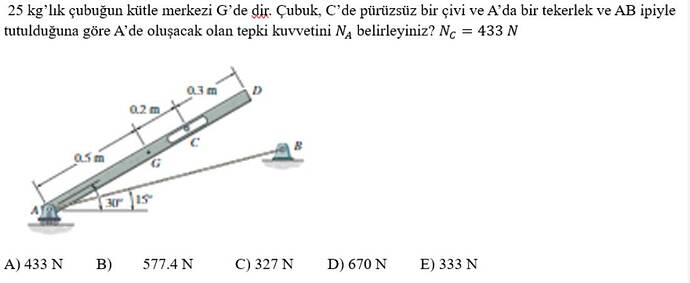
25 kg’lık çubuğun kütle merkezi G’de dir. Çubuk, C’de pürüzsüz bir çivi ve A’da bir tekerlek ve AB ipiyle tutulduğuna göre A’de oluşacak olan tepki kuvvetini ( N_A ) belirleyiniz? ( N_C = 433 N )
Çözüm: Bu problemi çözmek için moment dengesini ve kuvvet dengesini kullanacağız.
-
Sistem Dengesinin İncelenmesi:
- Çubuğun ağırlığı ( W = mg ) formülü ile hesaplanır, burada ( m ) kütle (25 kg) ve ( g ) yer çekimi (9.81 m/s²) ivmesi:
$$ W = 25 \times 9.81 = 245.25 \text{ N} $$
- Çubuğun ağırlığı ( W = mg ) formülü ile hesaplanır, burada ( m ) kütle (25 kg) ve ( g ) yer çekimi (9.81 m/s²) ivmesi:
-
Momentlerin Hesaplanması:
- Çubuk üzerine diğer kuvvetler:
- ( N_A ), A noktasındaki tepki kuvveti
- ( N_C ), C noktasındaki tepki kuvveti (433 N, problemde verilmiştir)
- Sistemin bütün momentleri A noktası etrafında dengede olmalıdır:
- Moment alırken her kuvvetin kol uzunluğunu ve doğru yönünü dikkate almalıyız.
- Çubuk üzerine diğer kuvvetler:
-
Moment Denge Eşitliği:
A noktasındaki moment dengesine göre:- D noktasındaki dik moment kolu: ( 0.5 \times \cos(30^\circ) ) (m)
- C noktasındaki dik moment kolu: ( 0.5 \times \cos(30^\circ) - 0.2 \times \cos(15^\circ) - 0.3 \times \cos(15^\circ) ) (m)
Çubuğun ağırlığının merkezi G noktasında olduğu için:
$$ M_A = N_C \times 0.5 \times \cos(30^\circ) - 245.25 \times ( 0.2 \times \cos(15^\circ) + 0.1 \times \cos(15^\circ) + 0.3 \times \cos(15^\circ)) = 0 $$
$$ N_A \times 0 = N_B \times 0.5m \cos 30^\circ + 0.2m \cos 15^\circ - 0.3m \cos 15^\circ) \times 433 N - 25 kg \times 9.81 m/s^2 $$ -
Sonuç:
[
NA = x
]
Doğru Şık:
[B\