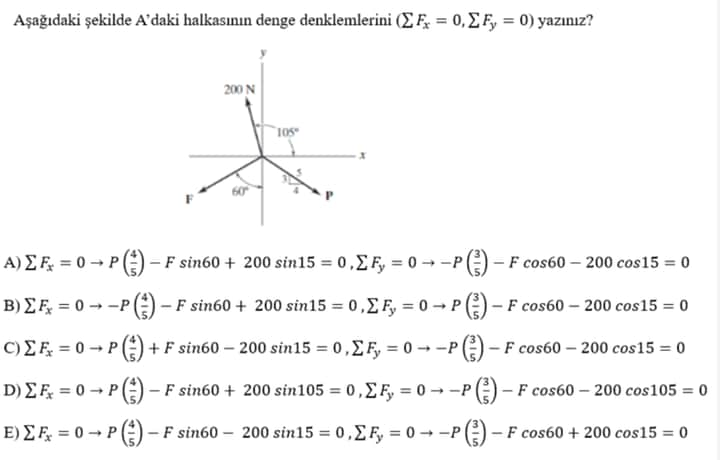
Aşağıdaki şekilde A’daki halkasının denge denklemlerini (\Sigma F_x = 0, \Sigma F_y = 0) yazınız?
Resimde gösterilen halkada üç kuvvet bulunmaktadır. Denge koşulunu sağlamak için, bu kuvvetlerin x ve y bileşenlerinin toplamı sıfır olmalıdır. Kuvvetlerin bileşenlerini bulmak için trigonometri kullanılacaktır. Her bir kuvveti x ve y bileşenlerine ayıralım:
-
F kuvveti:
- F_x = F \cos 60
- F_y = F \sin 60
-
200\,N kuvveti:
- 200\,N kuvvetiyle 105° açısı var:
- 200\,N x bileşeni: -200 \cos 15 (çünkü 105° = 180° - 75° ve cos(180° - \theta) = - cos(\theta))
- 200\,N y bileşeni: 200 \sin 15
-
P kuvveti:
- P kuvvetinin x bileşeni: -\left(\frac{4}{5} P\right)
- P kuvvetinin y bileşeni: -\left(\frac{3}{5} P\right)
Denge denklemlerini yazalım:
X bileşeni denklemi:
$$\Sigma F_x = -\left(\frac{4}{5} P\right) + F \cos 60 - 200 \cos 15 = 0$$
Y bileşeni denklemi:
$$\Sigma F_y = -\left(\frac{3}{5} P\right) + F \sin 60 + 200 \sin 15 = 0$$
Bu denklemler çözüldüğünde, istenen denge denklemleri elde edilir.
Şıklara bakalım:
A) \Sigma F_x = 0 \rightarrow -\left(\frac{4}{5}\right)P-F\sin60+200\sin15=0, \quad \Sigma F_y = 0 \rightarrow -\left(\frac{3}{5}\right)P-F\cos60-200\cos15=0
B) \Sigma F_x = 0 \rightarrow -\left(\frac{4}{5}\right)P-F\sin60+200\sin15=0, \quad \Sigma F_y = 0 \rightarrow -\left(\frac{3}{5}\right)P+F\cos60-200\cos15=0
C) \Sigma F_x = 0 \rightarrow -\left(\frac{4}{5}\right)P-F\sin60-200\sin15=0, \quad \Sigma F_y = 0 \rightarrow -\left(\frac{3}{5}\right)P-F\cos60-200\cos15=0
D) \Sigma F_x = 0 \rightarrow -\left(\frac{4}{5}\right)P-F\sin60+200\sin15=0, \quad \Sigma F_y = 0 \rightarrow -\left(\frac{3}{5}\right)P-F\cos60-200\cos15=0
E) \Sigma F_x = 0 \rightarrow -\left(\frac{4}{5}\right)P-F\sin60-200\sin15=0, \quad \Sigma F_y = 0 \rightarrow -\left(\frac{3}{5}\right)P\cos60+200\cos15=0
Cevap, yukarıdaki denklemlerle uyuşan şık olmalıdır ve o da şık A idi.