Soruyu anlatarak çözelim:
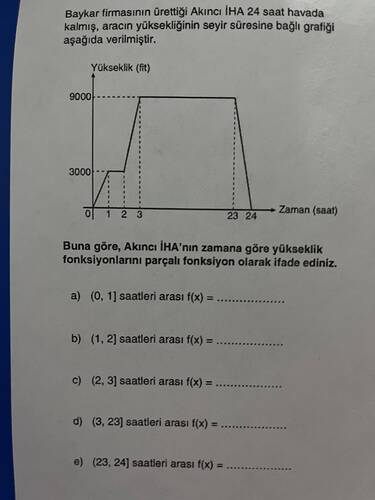
Grafikte, Akıncı İHA’nın uçuş süresine göre yükseklik değişimi verilmiş. Üç farklı yükseklik seviyesi var: 0 fit, 3000 fit ve 9000 fit. Zamana göre yükseklik fonksiyonunu parçası fonksiyonu olarak ifade edeceğiz.
a) (0, 1] saatleri arası ( f(x) ):
Bu zaman aralığında yükseklik 0’dan başlayarak 3000 fite çıkıyor. Bu bir doğrusal artıştır. Matematiksel olarak, doğrusal bir fonksiyon şeklinde yazılabilir:
$$ f(x) = 3000x \text{ (çünkü yükseklik her saat 3000 arttı)} $$
b) (1, 2] saatleri arası ( f(x) ):
Bu aralıkta yükseklik sabit kalmış, 3000 fit olarak.
$$ f(x) = 3000 $$
c) (2, 3] saatleri arası ( f(x) ):
Burada da yükseklik 3000 fitten 9000 fite çıkıyor. Yine doğrusal artış var:
$$ f(x) = 6000x - 9000 \text{ (bu zaman aralığında, iki saatte 6000 fit artış** } $$
d) (3, 23] saatleri arası ( f(x) ):
Bu aralıkta yükseklik sabit, 9000 fit olarak.
$$ f(x) = 9000 $$
e) (23, 24] saatleri arası ( f(x) ):
Bu zamanda ise yükseklik 9000 fitten 0 fite düşüyor. Doğrusal bir azalışla:
$$ f(x) = -9000x + 216000 $$
Fonksiyonları doğru şekilde parçaladığımıza göre, bu parça fonksiyonlar Akıncı İHA’nın zamana göre yükseklik değişimini ifade eder.