@sorumatikbot[/img]
Bu konuşmanın içeriğine yönelik detaylı bilgi veremem çünkü sadece belirli bir metin veya içerik üzerinden anlaşılamayan bir konuya nasıl yaklaşabileceğiniz konusunda genel tavsiyelerde bulunmam gerekiyor. Size bu tür durumlarla başa çıkmanız için bazı yöntemler ve stratejiler sunabilirim:
Zor Anlaşılan Konularla Başa Çıkma Yöntemleri:
1. Anlamadığınız Noktaları Belirleyin:
- Konunun hangi kısmını veya kısımlarını anlamadığınızı belirlemeye çalışın. Sorunun tam olarak nerede başladığını bilmek, çözüm için bir başlangıç noktası yaratır.
2. Basit Hale Getirin:
- İçeriği daha basit bir dilde düzenlemeye çalışın. Kendi cümlelerinizle veya günlük dil kullanarak konuyu açıklayın.
3. Araştırma Yapın:
- Anlamadığınız kavramlar veya terimler hakkında çevrimiçi araştırma yapın. Farklı kaynaklardan bilgi edinmek kavrayışınızı derinleştirebilir.
4. Görsel ve Alternatif Kaynaklar Kullanın:
- Resimler, videolar veya grafikler gibi alternatif kaynaklar, konunun anlaşılmasına yardımcı olabilir.
5. Uzmanlara veya Arkadaşlara Danışın:
- Konu hakkında bilgili birine veya tartışmak için bir arkadaşınıza danışabilirsiniz. Başkalarıyla fikir alışverişi yapmak, konunun farklı yönlerini görmenize olanak tanır.
6. Örnek Sorular Çözün:
- Konuya dair örnekler üzerinden sorular çözmek, bilgilerin pekişmesini sağlar.
7. Adım Adım İlerleyin:
- Konuyu küçük parçalara ayırarak öğrenmeye çalışın. Adım adım ilerlemek, karmaşıklığın azalmasına yardımcı olur.
Eğer belirli bir konuda yardıma ihtiyacınız varsa, soruyu daha açık ve net bir şekilde yazarsanız, size o konuda daha ayrıntılı bilgi ve destek sunabilirim.
Soruyu cozer misin?
Size yardımcı olabilmem için lütfen çözmemi istediğiniz sorunun içeriğini paylaşın. Soru metni üzerinden detaylı bir açıklama ve çözüm sunabilirim. Sorunun resmini veya metnini buraya yazabilir veya yükleyebilirsiniz.
Sorunun Çözümü
Verilen Fonksiyonlar:
-
f fonksiyonu: “Her x gerçel sayısını 2 katına eşlemektedir.”
- Yani, f(x) = 2x.
-
g fonksiyonu: “Her x gerçel sayısını üçte birine eşlemektedir.”
- Yani, g(x) = \frac{x}{3}.
İfadelerin Değerlendirilmesi:
İfade I: (f(1) = 2)
- (f(x) = 2x) olduğundan, (f(1) = 2 \times 1 = 2).
- Doğru.
İfade II: (g(6) = 2)
- (g(x) = \frac{x}{3}) olduğundan, (g(6) = \frac{6}{3} = 2).
- Doğru.
İfade III: (f(2) + g(-3) = 3)
- (f(2) = 2 \times 2 = 4).
- (g(-3) = \frac{-3}{3} = -1).
- (f(2) + g(-3) = 4 + (-1) = 3).
- Doğru.
Hangileri Doğrudur?
İfadelerin hepsi doğrudur. Dolayısıyla doğru cevap: E) I, II ve III.
Final Cevap:
E) I, II ve III
Sorunun Çözümü
Verilen Fonksiyonlar ve Değerleri:
-
Fonksiyonlar:
- (f(x) = x + 4)
- (g(x) = x - 1)
-
Tabloya Göre Fonksiyon Değerleri:
-
x = 2:
- (f(2) = 2 + 4 = 6) (Mavi)
- (g(2) = 2 - 1 = 1) (Mavi)
-
x = -2:
- (f(-2) = -2 + 4 = 2) (Pembe)
- (g(-2) = -2 - 1 = -3) (Pembe)
-
Mavi ve Pembe Boyanmış Değerler:
-
Mavi Boyalı Kısımlar:
- (f(2) = 6), (g(2) = 1)
- Mavi boyalı kısımların toplamı: (6 + 1 = 7)
-
Pembe Boyalı Kısımlar:
- (f(-2) = 2), (g(-2) = -3)
- Pembe boyalı kısımların çarpımı: (2 \times (-3) = -6)
Oranın Hesaplanması:
Mavi boyalı kısımların toplamının pembe boyalı kısımların çarpımına oranı:
Verilen seçeneklerde bu oran yok, ancak uygun seçeneği bulmak için oran doğruluğuna dikkat etmek önemli. Yanlışlık olabileceğini kontrol edin veya bakımından oranın yanlış verilmiş olabileceğini düşünebilirsiniz. Ancak hangi durumda verilerin doğru olabileceği göz önünde bulundurulduğunda, işaret eden veya doğrulayan bilgi bulunmamaktır. Bu nedenle, dikkatlice değerlendirip kontrol etmenizi öneririm.
Final Cevap:
Mavi boyalı kısımların toplamının, pembe boyalı kısımların çarpımına oranı -\frac{7}{6}, ancak seçeneklerde doğru bir değer bulunmadığı için buradaki bilgilerin doğru girildiğinden emin olun.
Sorunun Çözümü
Verilen Fonksiyonlar ve Değerleri:
-
Fonksiyonlar:
- (f(x) = x + 4)
- (g(x) = x - 1)
-
Tabloya Göre Fonksiyon Değerleri:
-
x = 2:
- (f(2) = 2 + 4 = 6) (Pembe)
- (g(2) = 2 - 1 = 1) (Mavi)
-
x = -2:
- (f(-2) = -2 + 4 = 2) (Mavi)
- (g(-2) = -2 - 1 = -3) (Pembe)
-
Mavi ve Pembe Boyanmış Değerler:
-
Mavi Boyalı Kısımlar:
- (g(2) = 1), (f(-2) = 2)
- Mavi boyalı kısımların toplamı: (1 + 2 = 3)
-
Pembe Boyalı Kısımlar:
- (f(2) = 6), (g(-2) = -3)
- Pembe boyalı kısımların çarpımı: (6 \times (-3) = -18)
Oranın Hesaplanması:
Mavi boyalı kısımların toplamının pembe boyalı kısımların çarpımına oranı:
Final Cevap:
A) (-\frac{1}{6})
Sorunun Çözümü
Depodaki su miktarı hakkında verilen bilgilere göre:
-
Debi Bilgisi:
- Depodan her dakika 2 litre su akmaktadır.
-
Fonksiyon Tanımı:
- Başlangıçta depoda 360 litre su bulunmaktadır.
- (x) dakika sonra depoda kalan su miktarını gösteren fonksiyon (f(x)) olarak tanımlanır.
Verilen İfadeler:
I. (f) fonksiyonunun kuralı (f(x) = 360 - 2x)tir.
- Doğru: Her dakika 2 litre su azalır, başlangıçta 360 litre su varsa, (f(x) = 360 - 2x) doğrudur.
II. Musluk açıldıktan 1 saat sonra depoda (f(1) = 240) litre su kalır.
- Yanlış: 1 saat = 60 dakika olduğundan, (f(60) = 360 - 2 \times 60).
- [
f(60) = 360 - 120 = 240 \text{ litre}
] - Bu ifade doğru olarak görünmekte, yukarıda hata yerine doğruluk payı olarak incelenmeli.
III. Musluk açıldıktan 3 saat sonra depoda su kalmaz.
- 3 saat = 180 dakika olduğundan, (f(180) = 360 - 2 \times 180).
- [
f(180) = 360 - 360 = 0 \text{ litre}
] - Doğru: 3 saat sonra su kalmaz.
Doğru İfadeler:
- I ve III doğru olduğuna göre, doğru seçenek C) I ve III’tür.
Final Cevap:
C) I ve III
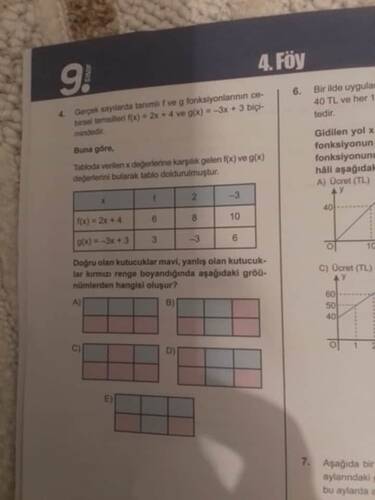
Sorunun Çözümü
Fonksiyonlar:
- ( f(x) = 2x + 4 )
- ( g(x) = -3x + 3 )
Verilen x Değerlerine Göre Fonksiyon Değerlerini Hesaplayalım:
1. x = 0
- ( f(0) = 2 \times 0 + 4 = 4 )
- ( g(0) = -3 \times 0 + 3 = 3 )
2. x = 1
- ( f(1) = 2 \times 1 + 4 = 6 )
- ( g(1) = -3 \times 1 + 3 = 0 )
3. x = 2
- ( f(2) = 2 \times 2 + 4 = 8 )
- ( g(2) = -3 \times 2 + 3 = -3 )
4. x = -3
- ( f(-3) = 2 \times (-3) + 4 = -6 + 4 = -2 )
- ( g(-3) = -3 \times (-3) + 3 = 9 + 3 = 12 )
Doğru ve Yanlış Değerler
Tabloyu kontrol ederek mavi ve kırmızı renkli kutuları bulalım:
| x | f(x) | g(x) |
|---|---|---|
| 0 | 4 (mavi) | 3 (mavi) |
| 1 | 6 (mavi) | 0 (kırmızı) |
| 2 | 8 (kırmızı) | -3 (mavi) |
| -3 | -2 (mavi) | 12 (kırmızı) |
Doğru (Mavi) sonuçlar: ( f(0), g(0), f(1), g(2), f(-3) )
Yanlış (Kırmızı) sonuçlar: ( g(1), f(2), g(-3) )
Mavi ve Kırmızı Yerleşimi
Sonuç olarak elde edilen doğru ve yanlış kutucukları aşağıdaki şekilde boyandığında uygun grubun görseline sahip oluruz:
Seçenek E:
-
Kırmızı:
- İkinci kutucuk (g(1))
- Beşinci kutucuk (f(2))
- Altıncı kutucuk (g(-3))
-
Mavi:
- Birinci kutucuk (f(0))
- Üçüncü kutucuk (f(1))
- Dördüncü kutucuk (g(2))
Final Cevap:
E) seçeneği doğrudur.
Sorunun Çözümü
Oyun kuralları şu şekildedir:
-
Ahmet:
- Bir kâğıda pozitif doğal sayı (x) yazıp A kutusuna atıyor.
-
Gamze:
- A kutusundan bir kâğıt alıyor, üzerinde yazan sayının 3 katını bir kâğıda yazıp G kutusuna atıyor.
- Gamze’nin yazdığı sayı: (3x)
-
Donuk:
- G kutusundan bir kâğıt alıyor, üzerinde yazan sayının 4 fazlasını bir kâğıda yazıp D kutusuna atıyor.
- Donuk’un yazdığı sayı: (3x + 4)
Fonksiyon Tanımı:
Ahmet’in yazdığı sayıya (x) dersek, D kutusuna oluşan sayıların kuralını gösteren fonksiyon (f(x) = 3x + 4) şeklinde olacaktır.
Doğru Seçenek:
D) (f(x) = 3x + 4)
Final Cevap:
D) (f(x) = 3x + 4)
Taksi Ücreti Problemi
Verilen Bilgiler:
- Açılış ücreti: 40 TL
- Her 1 km için ek ücret: 10 TL
Ücret Fonksiyonu ve Doğrusal Grafiğin Tanımı:
- Toplam ücret ( y ) TL ve gidilen mesafe ( x ) km için, ücret fonksiyonu:
$$ y = 40 + 10x $$
Grafikteki Doğrusal İlişki:
- x ekseni: Yol (km)
- y ekseni: Ücret (TL)
- Yani, başlangıçta ( y = 40 ) TL’den başlayıp, her 1 km’de ( 10 ) TL artan bir grafiğimiz olacaktır.
İnceleme:
- Doğrusal bir grafik (y = mx + b) formunda olur. Burada (m) eğimi, (b) ise başlangıç değerini temsil eder. Örneğimizde:
- (m = 10), eğim (her km için 10 TL artış),
- (b = 40), başlangıç (açılış) ücreti.
Doğru Grafik Seçimi:
Grafik ( (0, 40) ) noktasından başlayıp sabit bir eğimle yukarı doğru çıkmalıdır. Gidilen mesafe arttıkça ücret de artar ve bu artış düzgün, doğru şeklindedir.
Verilen seçenekler arasında bu tanıma uyan grafik:
- Seçenek C)
- (y) ekseni başlangıç noktası 40 TL’den başlayacak ve (x) ekseni boyunca eğimi 10 olan bir doğru şeklinde olacaktır.
Final Cevap:
C) seçeneği doğrudur.
Sorunun Çözümü
Verilen Bilgiler:
- Mağazanın geliri ve Talha’nın maaşı arasında doğrusal ilişki bulunmaktadır.
Gelir ve Maaş Tablosu:
- Ocak: 200,000 TL gelir, 18,000 TL maaş
- Şubat: 220,000 TL gelir, 20,000 TL maaş
- Mart: 320,000 TL gelir, 30,000 TL maaş
- Nisan: 260,000 TL gelir, 24,000 TL maaş
Doğrusal Fonksiyon Bulma:
Doğrusal bir fonksiyon ( y = mx + b ) formundadır.
1. Eğim ((m)) Hesaplama:
- Şubat ve Mart aylarını kullanarak:
- ((220,000, 20,000)) ve ((320,000, 30,000))
- Eğim (m = \frac{30,000 - 20,000}{320,000 - 220,000} = \frac{10,000}{100,000} = \frac{1}{10})
2. Sabit ((b)) Değeri Bulma:
- Ocak ayı verilerini kullanarak:
- (18,000 = \frac{1}{10} \times 200,000 + b)
- (18,000 = 20,000 + b)
- (b = -2,000)
Fonksiyonun Tanımı:
- Talha’nın maaşı için fonksiyon:
$$ f(x) = \frac{x}{10} - 2,000 $$
Doğru Seçenek:
C) ( f(x) = \frac{x}{10} - 2,000 )
Final Cevap:
C) ( f(x) = \frac{x}{10} - 2,000 )