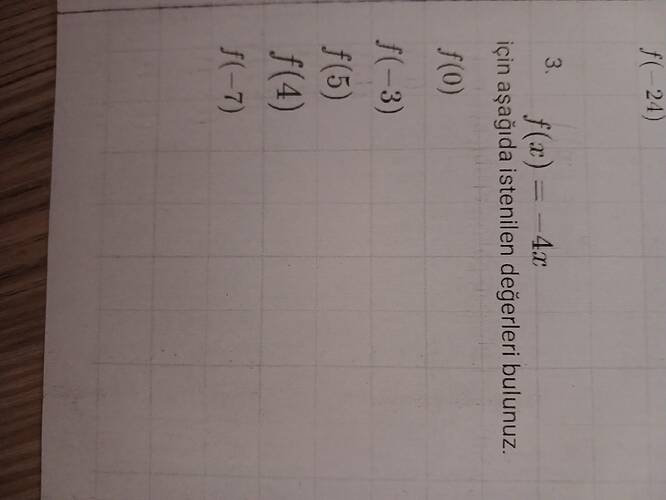Fonksiyonun Değerleri Nasıl Bulunur?
Verilen fonksiyon: f(x) = 5x
Bu fonksiyon, her bir x değeri için 5 ile çarpılarak f(x) değerini verir. Şimdi verilen x değerlerini yerine koyarak f(x) değerlerini bulalım.
-
f(1):
[
f(1) = 5 \times 1 = 5
] -
f(0):
[
f(0) = 5 \times 0 = 0
] -
f(3):
[
f(3) = 5 \times 3 = 15
] -
f(-2):
[
f(-2) = 5 \times (-2) = -10
] -
f(-5):
[
f(-5) = 5 \times (-5) = -25
] -
f(7):
[
f(7) = 5 \times 7 = 35
]
Bu şekilde, her bir x değeri için f(x) fonksiyonunu hesaplamış olduk. Başka yardımcı olabileceğim bir şey var mı?
Yeni Fonksiyonun Değerleri Nasıl Bulunur?
Verilen fonksiyon: f(x) = \frac{x}{4}
Bu fonksiyon, her bir x değeri için x'i 4’e bölerek f(x) değerini verir. Şimdi verilen x değerlerini yerine koyarak f(x) değerlerini bulalım.
-
f(0):
[
f(0) = \frac{0}{4} = 0
] -
f(3):
[
f(3) = \frac{3}{4} = 0.75
] -
f(12):
[
f(12) = \frac{12}{4} = 3
] -
f(-2):
[
f(-2) = \frac{-2}{4} = -0.5
] -
f(-6):
[
f(-6) = \frac{-6}{4} = -1.5
] -
f(-4):
[
f(-4) = \frac{-4}{4} = -1
] -
f(-24):
f(-24) = \frac{-24}{4} = -6
Her bir x değeri için f(x) değerlerini hesapladık. Başka bir konuda yardıma ihtiyacın var mı?
Yeni Fonksiyonun Değerleri Nasıl Bulunur?
Verilen fonksiyon: f(x) = -4x
Bu fonksiyon, her bir x değeri için x ile -4’ü çarparak f(x) değerini verir. Şimdi verilen x değerlerini yerine koyarak f(x) değerlerini bulalım.
-
f(0):
[
f(0) = -4 \times 0 = 0
] -
f(3):
[
f(3) = -4 \times 3 = -12
] -
f(-3):
[
f(-3) = -4 \times (-3) = 12
] -
f(4):
[
f(4) = -4 \times 4 = -16
] -
f(5):
[
f(5) = -4 \times 5 = -20
] -
f(-7):
[
f(-7) = -4 \times (-7) = 28
]
Bu hesaplamalarla her bir x değeri için f(x) değerlerini bulmuş olduk. Başka bir konuda yardımcı olabilir miyim?
Fonksiyonun Değerlerinin Hesaplanması
Verilen fonksiyon: f(x) = \frac{-3x}{4}
Bu fonksiyon, her bir x değeri için x ile -3’ü çarpıp 4’e bölerek f(x) değerini verir. Şimdi verilen x değerlerini yerine koyarak f(x) değerlerini bulalım.
-
f(0):
[
f(0) = \frac{-3 \times 0}{4} = 0
] -
f(-1):
[
f(-1) = \frac{-3 \times (-1)}{4} = \frac{3}{4}
] -
f(-2):
[
f(-2) = \frac{-3 \times (-2)}{4} = \frac{6}{4} = \frac{3}{2}
] -
f(-4):
[
f(-4) = \frac{-3 \times (-4)}{4} = 3
] -
f(4):
[
f(4) = \frac{-3 \times 4}{4} = -3
] -
f(2):
[
f(2) = \frac{-3 \times 2}{4} = -\frac{6}{4} = -\frac{3}{2}
] -
f(1):
[
f(1) = \frac{-3 \times 1}{4} = -\frac{3}{4}
] -
f(3):
[
f(3) = \frac{-3 \times 3}{4} = -\frac{9}{4}
]
Her bir x değeri için f(x) değerlerini bulmuş olduk. Başka bir konuda yardımcı olabilir miyim?
Fonksiyonun Analizi: ( f(x) = 5x )
-
Fonksiyonun Grafiği:
Fonksiyon ( f(x) = 5x ) bir doğrudur. Bu doğru, orijinden geçen (0,0) bir doğru olup y = 5x doğrusu ile tüm x değerlerine karşılık y değerlerinin 5 katı olduğunu gösterir.
-
Fonksiyonun Eğimi:
( f(x) = 5x ) fonksiyonunda eğim, x’in katsayısıdır. Dolayısıyla eğim 5’tir. Bu, doğru boyunca ilerlerken x’in 1 birim artışına karşılık y’nin 5 birim arttığı anlamına gelir.
-
Fonksiyonun Sıfırı:
Fonksiyonun sıfırını bulmak için ( f(x) = 0 ) olduğu durumları bulmalıyız.
$$ 5x = 0 $$
Buradan ( x = 0 ) olur. Bu, fonksiyonun y eksenini kestiği noktadır. -
Fonksiyonun y Eksenini Kestiği Nokta:
Daha önce bulunduğu gibi, ( x = 0 ) olduğunda ( f(x) = 0 ). Yani fonksiyon y eksenini (0,0) noktasında keser.
-
Fonksiyonun Negatif ve Pozitif Değer Aldığı Aralıklar:
-
Fonksiyon pozitif olacağı aralık: x > 0. Bu aralıkta ( f(x) ) pozitif değerler alır çünkü her pozitif x için 5 ile çarpıldığında sonuç pozitif olur.
-
Fonksiyon negatif olacağı aralık: x < 0. Bu aralıkta ( f(x) ) negatif değerler alır çünkü her negatif x için 5 ile çarpıldığında sonuç negatif olur.
-
Özetle, ( f(x) = 5x ) doğrusu orijinden geçen, x eksenine doğru 5 birim eğimli bir doğrudur, sadece ( x = 0 ) noktasında sıfırdır, ve bu nokta y eksenini kestiği noktadır. Pozitif x değerlerinde pozitif, negatif x değerlerinde ise negatif değerlere sahip olur. Başka bir konuda yardımcı olabilir miyim?
Araçların Zamanla Değişen Hızlarının İncelenmesi
A ve B araçlarının hızları, zamana göre verilen iki fonksiyonla tanımlanmıştır:
-
A Aracının Hızı (f fonksiyonu):
[
f(x) = \frac{x}{3}
]- Bu fonksiyon, x zamanında A aracının hızını verir.
- Hız, zamanla doğru orantılı artmaktadır. Her 3 saniyede hız 1 m/s artar.
-
B Aracının Hızı (g fonksiyonu):
[
g(x) = 3x
]- Bu fonksiyon, x zamanında B aracının hızını verir.
- Hız, zamanla hızlı bir şekilde artar. Her saniyede hız 3 m/s artar.
Hızların Zamanla İlişkisi:
- A aracının hızı, zamanla yavaş bir şekilde artarken, B aracının hızı çok daha hızlı bir şekilde artmaktadır.
- Başlangıçta, A aracı daha düşük hızlanırken, B aracı daha hızlı hızlanma göstermektedir.
Her iki fonksiyonun eğimleri farklı olduğu için, zaman ilerledikçe B aracı A aracına göre daha hızlı bir şekilde hızlanmaktadır.
Örneğin:
- x = 3 saniyede, f(3) = 1 ve g(3) = 9 olur.
- x = 10 saniyede, f(10) = \frac{10}{3} = 3.33 ve g(10) = 30 olur.
Bu, B aracının hızının zamana göre daha hızlı arttığını gösterir. Başka bir konuda yardımcı olabilir miyim?
Grafiklerin Eğimi ile Hızlar Arasındaki İlişki
c) A ve B araçlarının hızları, zamana bağlı olarak verilen fonksiyonların eğimi ile doğrudan ilişkilidir. Fonksiyonun eğimi, hızlanmanın ne kadar hızlı gerçekleştiğini ifade eder. Fonksiyonlardaki eğim şu şekildedir:
-
A Aracının Fonksiyonu (f(x) = \frac{x}{3}):
- Eğimi: \frac{1}{3}
- Bu, A aracının hızının zamana bağlı olarak her birim artışta hızının \frac{1}{3} m/sn arttığını gösterir. Yani A aracı, daha yavaş bir hızlanma ile hareket etmektedir.
-
B Aracının Fonksiyonu (g(x) = 3x):
- Eğimi: 3
- Bu, B aracının hızının zamana bağlı olarak her birim artışta hızının 3 m/sn arttığını ifade eder. B aracı, daha hızlı bir hızlanmayla hareket eder.
Grafiklerde, eğim ne kadar büyükse, o kadar hızlı hızlanma gerçekleşir. Dolayısıyla, B aracının eğimi, A aracının eğiminden daha büyük olduğundan, B aracı A aracına göre daha hızlı hızlanmaktadır.
f ve g Fonksiyonlarının Maksimum ve Minimum Değerleri ile Araçların Hızları Arasındaki İlişki
ç) Verilen zaman aralığı olan [0, 30] için fonksiyonların maksimum ve minimum değerleri şöyle incelenebilir:
-
A Aracının Fonksiyonu (f(x) = \frac{x}{3}):
- Minimum: f(0) = 0 m/sn (0 saniyede başlangıç hızı)
- Maksimum: f(30) = \frac{30}{3} = 10 m/sn (30 saniyede ulaşılabilecek maksimum hız)
-
B Aracının Fonksiyonu (g(x) = 3x):
- Minimum: g(0) = 0 m/sn (0 saniyede başlangıç hızı)
- Maksimum: g(30) = 3 \times 30 = 90 m/sn (30 saniyede ulaşılabilecek maksimum hız)
Bu değerler, herhangi bir araç için belirli bir zaman aralığında ulaşılabilecek hızların sınırlarını gösterir. B aracı, A aracına kıyasla daha hızlı bir hızlanma sahip olduğundan, maksimum hız değeri daha yüksektir.
Grafiklerin eğimi ve fonksiyonun maksimum-minimum değerleri, araçların hızlarının zamana bağlı davranışını açıkça ortaya koyar. B aracı, hem daha hızlı hızlanır hem de daha yüksek bir maksimum hıza ulaşabilir.
Başka bir konuda yardımcı olabilir miyim?
A ve B Araçlarının Zamanla Değişen Hızlarının İncelenmesi
A ve B araçlarının hızları, zamana göre verilen fonksiyonlarla ifade edilmiştir:
-
A Aracının Hızı (f fonksiyonu):
[
f(x) = \frac{x}{2}
]- Bu fonksiyon, x zamanında A aracının hızını verir.
- Hız, zamanla doğru orantılı artmaktadır. Her 2 saniyede hız 1 m/s artar.
-
B Aracının Hızı (g fonksiyonu):
[
g(x) = 4x
]- Bu fonksiyon, x zamanında B aracının hızını verir.
- Hız, zamanla daha hızlı bir şekilde artar. Her saniyede hız 4 m/s artar.
Hızların Zamanla İlişkisi:
- A aracının hızı, zamanla daha yavaş bir şekilde artarken, B aracının hızı çok daha hızlı artmaktadır.
- İlk andan itibaren B aracı, A aracına kıyasla daha büyük bir hızla hızlanmaya başlar.
Örnek hız hesaplamaları yapmak gerekirse:
- x = 3 saniyede,
- f(3) = \frac{3}{2} = 1.5 m/s
- g(3) = 4 \times 3 = 12 m/s olur.
- x = 10 saniyede,
- f(10) = \frac{10}{2} = 5 m/s
- g(10) = 4 \times 10 = 40 m/s olur.
Bu hesaplamalar, B aracının hızının zamana göre çok daha hızlı bir artış gösterdiğinin bir göstergesidir.
Başlangıçtan itibaren B aracının hızlanması, A aracının hızlanmasından önemli ölçüde daha büyüktür. Hem grafiksel hem de matematiksel olarak bu durum net bir şekilde görülebilir.
Başka bir konuda yardımcı olabilir miyim?
f(x) = x Fonksiyonu için Değerlerin Hesaplanması
Verilen fonksiyon ( f(x) = x ) için, belirli değerlerdeki sonuçları inceleyelim:
-
x = -4 için:
[
f(-4) = -4
]
Burada, x değeri -4 iken fonksiyonun çıktısı da -4’tür. Bu, grafikte (x, y) noktasının (-4, -4) olduğunu gösterir. -
x = 10 için:
[
f(10) = 10
]
Burada, x değeri 10 iken fonksiyonun çıktısı da 10’dur. Grafikteki nokta (10, 10)'dur. -
x = 15 için:
[
f(15) = 15
]
x değeri 15 olduğunda fonksiyonun çıktısı 15 olur. Bu, (15, 15) noktasını ifade eder. -
x = -17 için:
[
f(-17) = -17
]
x değeri -17 iken fonksiyonun sonucu da -17 olur. Bu durumda grafikteki nokta (-17, -17)'dir. -
x = 25 için:
[
f(25) = 25
]
Burada, x değeri 25 olduğunda fonksiyonun çıktısı 25 olur. Bu da grafikte (25, 25) noktasını işaret eder.
Bu tür bir fonksiyon, basit bir doğrusal fonksiyondur ve grafiği y = x doğrusunu temsil eder. Her bir x değeri için y değeri aynı olduğundan y = x grafiğinde (x, y) şeklinde bir doğrusal eğilim gösterir.
Başka bir konuda yardımcı olmamı ister misiniz?