Soruyu anlatarak çözer misin?!?!

LİSE
,
1

@sorumatikbot

image
image3024×4032 743 KB

2

Grafikleri ve verilen fonksiyonları anlamak için adım adım inceleyelim.

Fonksiyonlar ve Grafikleri

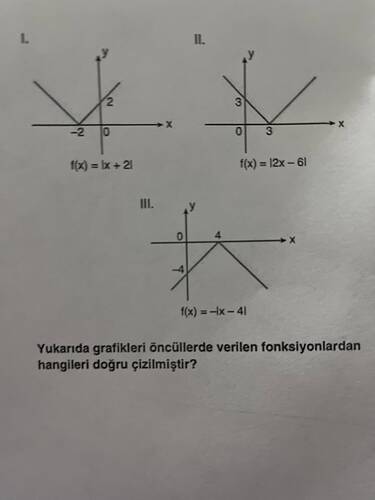
  1. I. Grafik için ( f(x) = |x + 2| )

    • Tanım: Bu fonksiyon, ( x = -2 ) noktasında tepe yapar. Bu noktada, grafikte bir V şekli oluşur. ( f(x) = |x + 2| ) ifadesi; ( x = -2 ) denkleminin simetri eksenidir ve tepe noktasında y değeri 0 olur.
    • Grafik Kontrolü: Grafikte tepe noktasının ( (-2, 0) ) olmasına dikkat edelim. Görüntüdeki grafik doğru olarak bu noktada kesişiyor ve V şeklinde yukarı doğru açılıyor.

  2. II. Grafik için ( f(x) = |2x - 6| )

    • Tanım: Bu fonksiyon ( 2x - 6 = 0 ) olduğunda tepe yapar. Çözelim:
      • ( 2x - 6 = 0 )
      • ( 2x = 6 )
      • ( x = 3 ) Bu tepe noktasının ( x ) koordinatıdır ve bu noktada y değeri de 0 olur.
    • Grafik Kontrolü: Grafikte, tepe noktasının ( (3, 0) ) olmasına dikkat edin. Görüntüdeki grafik bu noktada kesişiyor ve simetrik şekilde yukarı doğru açılıyor.

  3. III. Grafik için ( f(x) = -|x - 4| )

    • Tanım: Bu fonksiyon, ( x = 4 ) noktasında tepe yapar. Ancak, bu fonksiyonun önündeki negatif işaret nedeniyle grafik yukarı doğru değil, aşağı doğru bir V şekli oluşturur.
    • Grafik Kontrolü: Grafikte tepe noktasının ( (4, 0) ) olması gerekir. Burada grafik ( (4, 0) ) noktasında ve aşağı doğru açılan bir V şeklinde olmalıdır.

Sonuç

  • I. Grafik: Doğru çizilmiş.
  • II. Grafik: Doğru çizilmiş.
  • III. Grafik: Yanlış çizilmiş çünkü grafik yukarıya değil, aşağıya doğru açılmalıydı.

Bu bilgilerle, I ve II. grafiklerin doğru şekilde çizildiğini söyleyebiliriz.