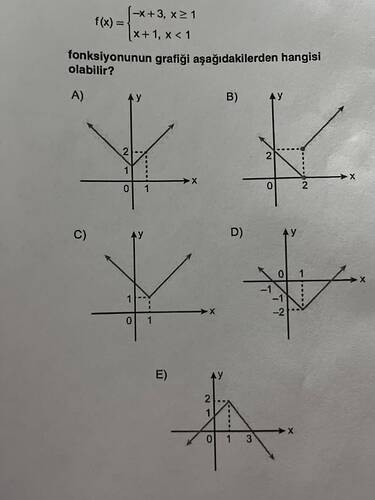
f(x) fonksiyonunun grafiği aşağıdakilerden hangisi olabilir?
Bu fonksiyon bir parçalı fonksiyondur ve iki farklı ifade ile tanımlanır:
- (x \geq 1) için (f(x) = -x + 3)
- (x < 1) için (f(x) = x + 1)
Adım 1: Grafiği Anlamak ve Çizmek
1. Bölge: (x \geq 1) için (f(x) = -x + 3)
- Bu ifade (x) doğrusu üzerindeki herhangi bir noktayı alıp onu negatif yapar ve 3 ekleyerek, bir y fonksiyonu oluşturur.
- (x = 1) için (f(x) = -1 + 3 = 2) noktasını verir.
- Eğimi (-1) olan bir doğrudur ve sola doğru eğimli olacaktır.
2. Bölge: (x < 1) için (f(x) = x + 1)
- Bu ifade klasik (y = x + 1) doğrusu olup ((x,y)) ilişkisini tanımlayan bir doğrusal fonksiyondur.
- (x = 0) için (f(x) = 0 + 1 = 1) noktasını verir.
- Eğimi (1) olan ve yukarı sağa doğru eğilen bir doğrudur.
Adım 2: Kesim Noktalarını Ele Almak
Fonksiyonun kesim noktalarını kontrol ederken:
- (x = 1) için (f(x)) noktası (x \geq 1) bölgesinden ((1,2)) noktasını,
- (x < 1) bölgesinden (x) değerine yaklaşır ve bu noktadaki değer ((1,2)) olacaktır. Bu da grafikte noktaların birleştiği yeri tanımlar.
Adım 3: Uygun Grafiği Seçmek
Verilen grafilere bakarak, kesim noktaları ve grafiklerin eğimlerini uygun şekilde kontrol edelim:
- Grafik (x = 1) noktasında ((1, 2)) noktasında birleşmelidir.
- Eğimi doğru tanımladığı ve verilen parçaları uygun şekilde birleştiren grafik (A) seçeneğidir.
Bu yüzden doğru cevap (A) seçeneğidir.