Belirttiğiniz konuşmanın konusu olarak aşağıdaki soruları sırayla çözebiliriz.
1. Soru
Çözüm:
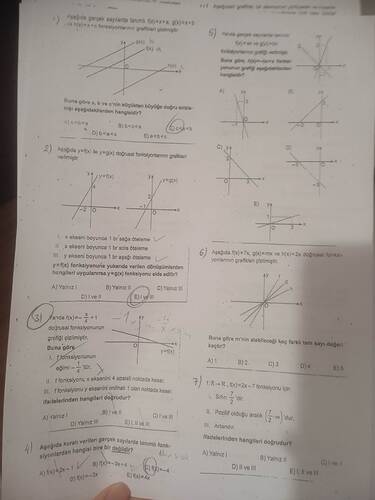
Verilen grafiklerden f(x) = ax + b, g(x) = x + b ve h(x) = x fonksiyonları çizilmiştir. Bu tür sorularda grafiğin y eksenini kesme noktası ve eğiminden faydalanırız.
- f(x) fonksiyonunun eğimi a olsun.
- g(x) fonksiyonunun eğimi 1’dir ve y eksenini b noktasında keser.
- h(x) fonksiyonu y = x doğrusudur ve eğimi 1’dir.
Grafik üzerindeki eğim ve y ekseni kesişimlerine göre sıralama yapılır, cevabı kontrol ediniz: ( c < a < b ).
2. Soru
Çözüm:
Verilen dönüşümlere göre f(x) ve g(x) fonksiyonları incelenir:
- f(x) fonksiyonunu x ekseni boyunca 1 birim sağa öteleme: ( f(x-1) )
- f(x) fonksiyonunu y ekseni boyunca 1 birim aşağıya öteleme: ( f(x) - 1 )
Dönüşümlerin hangileri uygulandığında g(x) fonksiyonu elde edilir kontrol edilmelidir. Cevabı kontrol ediniz: Yalnız I.
3. Soru
Çözüm:
f(x) = x / 3 - 1 doğrusunun grafiği incelenir:
- Eğimi 1/3’tür.
- x eksenini (0, -1) noktasında keser.
Sorunun diğer kısımlarıyla birlikte ele alındığında:
- I. Doğru
- II. Yanlış
- III. Doğru
Cevabınızı kontrol edin: I ve III.
4. Soru
Çözüm:
Her bir fonksiyonun türü ve eğimi bilinerek:
- f(x) = 2 doğrusal bir fonksiyondur, sabittir.
- f(x) = -3x doğru şeklindedir.
- f(x) = x/4 doğru şeklindedir.
Doğru seçeneğin hangisi olduğuna dikkat edilmelidir. Yanlış türde olanı bulunuz: ( f(x) = 3x ) eksik verilmiş olabilir.
5. Soru
Çözüm:
Verilen grafikteki eğim ve kesişim noktalarına göre hangi fonksiyonun kime ait olduğunu belirleme sorusu. m değeri bulunarak cevaba ulaşılır. Cevabı kontrol edin.
6. Soru
Çözüm:
a: y eksenine göre simetrildir.
b: Evensimetrik bir fonksiyondur.
c: Simetrilerle ilgili farklı özellikler incelenir. Cevabı kontrol edin.
7. Soru
Çözüm:
a, b, c seçenekleri verilen R → R :f(x)=2x−7 fonksiyonu için sıfır, pozitifliği ve artan/azalan olma durumu incelenir. Cevabı kontrol edin.
Bu şekilde her bir sorunun çözümünü adım adım inceleyebiliriz. Her adımda grafiğin analizine ve fonksiyonun dönüşümlerine dikkat etmek önemlidir.