Verilen Fonksiyonların Grafikleri ve Eğimi
a) G, H, K ve M Fonksiyonlarının Grafiğini Çiziniz
Verilen fonksiyonları inceleyelim:
-
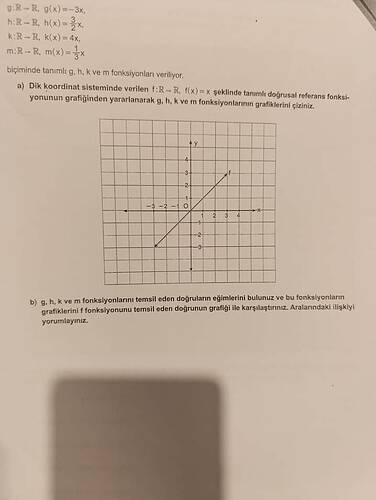
f(x) = x: Bu fonksiyon doğrusaldır ve eğimi 1’dir. y = x doğrusudur ve grafikte verilmiştir.
-
g(x) = -3x: Eğim -3 ve y-intersect olmadan grafik y = -3x doğrusu olacaktır. Bu doğru, x ekseni ile negatif y eğimiyle kesişiyor.
-
h(x) = (3/2)x: Eğim 3/2 olan bir doğrudur. Grafik, y = (3/2)x doğrusudur ve x eksenine göre pozitif bir açıyla yükselmektedir.
-
k(x) = 4x: Eğim 4 olan bir doğrudur. Grafik, y = 4x doğrusu olacak ve x eksenine göre oldukça dik bir yükselme gösterecektir.
-
m(x) = (1/3)x: Eğim 1/3 olan bir doğrudur. Grafik, y = (1/3)x doğrusu olacak ve x eksenine göre daha az dik bir yükselme gösterecektir.
b) Eğimler ve Grafikleri Karşılaştırma
Fonksiyonların eğimleri aşağıdaki gibidir:
- f(x) = x: Eğim = 1
- g(x) = -3x: Eğim = -3
- h(x) = (3/2)x: Eğim = 3/2
- k(x) = 4x: Eğim = 4
- m(x) = (1/3)x: Eğim = 1/3
Karşılaştırma:
-
Eğim İşaretleri: g(x) dışındaki tüm fonksiyonların eğimi pozitiftir. g(x)'in eğimi negatiftir, dolayısıyla bu doğrusu x eksenine göre aşağıya eğimlidir ve grafiği pozitif eğimden farklı bir yön gösterir.
-
Eğim Büyüklükleri: k(x) fonksiyonunun eğimi en büyüktür, bu da grafikte en dik açılı yükselme gösterdiği anlamına gelir. m(x) ise en küçük pozitif eğime sahiptir, bu nedenle grafiği en yatay görünen doğrudur. g(x) eğimi negatif olduğu için iniş yönündedir.
-
Referans Fonksiyon Olarak f(x) Grafiği: f(x) = x referans fonksiyonudur, ve dik koordinat sisteminde 45 derece açılı bir doğrusu temsil eder. Diğer fonksiyonların eğimleri bu doğrultuyla kıyaslanarak daha dik veya daha yatay oldukları değerlendirilmelidir.
Grafiksel olarak doğruları çizerken, her bir fonksiyonun kendi eğimi ve yeri ile eksenlerdeki kesişimleri dikkate alınarak uygun doğru çizimleri yapılmalıdır. Eğimin büyüklüğü ve işareti grafiklerin koordinat sistemindeki eğimini ve yönünü belirler.