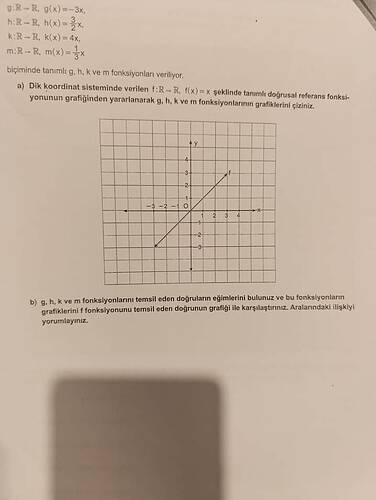
Görev: g, h, k ve m fonksiyonlarının grafikleri ve eğimleri
Cevap:
Verilen fonksiyonlar:
- ( g(x) = -3x )
- ( h(x) = \frac{3}{2}x )
- ( k(x) = 4x )
- ( m(x) = \frac{1}{3}x )
Referans fonksiyonu:
- ( f(x) = x )
Adım 1: Fonksiyonların grafikleri
- ( f(x) = x ) fonksiyonunun grafiği: Bu grafik, y = x doğrusu olup, 45 derece açıyla orijinden geçen bir doğrudur.
- ( g(x) = -3x ) fonksiyonunun grafiği: Eğimi -3 olan bu doğrusal grafik, y eksenine göre negatif eğime sahiptir. y = -3x doğrusu, orijinden geçer ve y eksenine dar bir açı yapar.
- ( h(x) = \frac{3}{2}x ) fonksiyonunun grafiği: Eğimi (\frac{3}{2}) olan bu grafik, f(x) = x doğrusuna daha dik bir açı yapar.
- ( k(x) = 4x ) fonksiyonunun grafiği: Eğimi 4 olan bu grafik, y eksenine oldukça dar bir açı yapar, f(x) = x doğrusuna göre daha dik.
- ( m(x) = \frac{1}{3}x ) fonksiyonunun grafiği: Eğimi (\frac{1}{3}) olan bu grafik, f(x) = x’e göre daha düzdür.
Adım 2: Eğimin belirlenmesi ve grafiklerin karşılaştırılması
Fonksiyonların eğimleri:
- ( g(x) ) için eğim: -3
- ( h(x) ) için eğim: (\frac{3}{2})
- ( k(x) ) için eğim: 4
- ( m(x) ) için eğim: (\frac{1}{3})
Karşılaştırma:
- Referans fonksiyonu ( f(x) = x )'in eğimi 1’dir.
- ( g(x) = -3x )'in eğimi negatiftir, bu nedenle grafik y = x’in eğimine ters yönde daha dik bir açıda olacaktır.
- ( h(x) = \frac{3}{2}x )'in eğimi 1’den büyüktür, bu nedenle grafik y = x’ten daha dik olacaktır.
- ( k(x) = 4x )'in eğimi 4’tür. Bu grafik y = x’ten çok daha dik olacaktır.
- ( m(x) = \frac{1}{3}x )'in eğimi 1’den küçüktür, bu nedenle grafik y = x’e göre daha yatık olacaktır.
Sonuç:
Grafikleri çizdiğinizde, her bir fonksiyonun eğimi ve yönü, referans fonksiyonu ( f(x) = x )'e kıyasla belirgin bir şekilde fark edecektir. Negatif eğim, negatif yöne diktir, pozitif eğim ne kadar büyükse, pozitif yönde o kadar diktir. Eğimin büyüklüğü, doğrunun y eksenine olan açısını belirler.