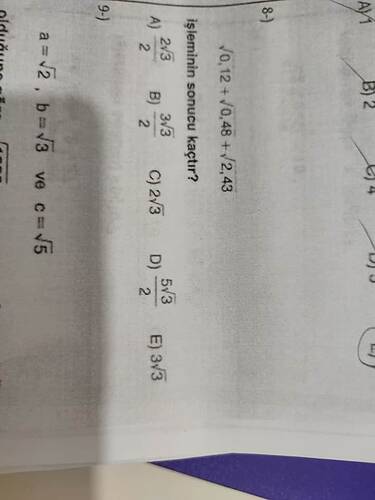
Görüntüdeki soruya bakalım:
$$ \sqrt{0.12} + \sqrt{0.48} + \sqrt{2.43} $$ işleminin sonucunu bulmamız gerekiyor.
Öncelikle kök ifadelerini sadeleştirerek başlayalım:
-
\sqrt{0.12} ifadesini sadeleştirirsek:
$$ 0.12 = \frac{12}{100} = \frac{3}{25} $$
$$ \sqrt{\frac{3}{25}} = \frac{\sqrt{3}}{5} $$ -
\sqrt{0.48} ifadesini sadeleştirirsek:
$$ 0.48 = \frac{48}{100} = \frac{12}{25} $$
$$ \sqrt{\frac{12}{25}} = \frac{\sqrt{12}}{5} = \frac{\sqrt{4 \times 3}}{5} = \frac{2\sqrt{3}}{5} $$ -
\sqrt{2.43} ifadesini sadeleştirirsek:
$$ 2.43 = \frac{243}{100} = \frac{81 \times 3}{100} $$
$$ \sqrt{\frac{243}{100}} = \frac{\sqrt{243}}{10} = \frac{\sqrt{81 \times 3}}{10} = \frac{9\sqrt{3}}{10} $$
Şimdi bu kök ifadeleri toplayalım:
$$ \frac{\sqrt{3}}{5} + \frac{2\sqrt{3}}{5} + \frac{9\sqrt{3}}{10} $$
İlk iki ifadeyi toplayalım:
$$ \frac{\sqrt{3}}{5} + \frac{2\sqrt{3}}{5} = \frac{3\sqrt{3}}{5} $$
Şimdi ise üçüncü ifade ile toplayalım:
$$ \frac{3\sqrt{3}}{5} + \frac{9\sqrt{3}}{10} $$
Bu ifadelerin paydalarını eşitleyelim:
$$ = \frac{6\sqrt{3}}{10} + \frac{9\sqrt{3}}{10} = \frac{15\sqrt{3}}{10} $$
Bu ifadenin sadeleştirilmiş hali:
$$ = \frac{3\sqrt{3}}{2} $$
Cevap şıkları arasında bu ifade, şıklardan biri olan B) \frac{3\sqrt{3}}{2} ile eşleşiyor.
Doğru cevap: B) \frac{3\sqrt{3}}{2}.
cevap b şıkkı