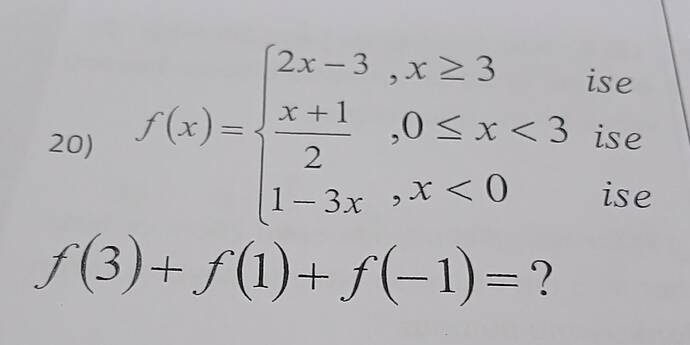Bu fonksiyonun toplamına bakalım:
Anahtar Kavram
Parçalı fonksiyon, tanımına göre farklı aralıklarda farklı ifadelerle tanımlanan bir fonksiyondur.
Temel Cevap
Fonksiyon ( f(x) ) üç parçalıdır:
- ( x \geq 3 ) için ( f(x) = 2x - 3 )
- ( 0 \leq x < 3 ) için ( f(x) = \frac{x + 1}{2} )
- ( x < 0 ) için ( f(x) = 1 - 3x )
Adım 1: ( f(3) )'ü Bul
- ( x = 3 ) için, ( 3 \geq 3 ) olduğundan:
[
f(3) = 2(3) - 3 = 6 - 3 = 3
]
Adım 2: ( f(1) )'i Bul
- ( x = 1 ) için, ( 0 \leq 1 < 3 ) olduğundan:
[
f(1) = \frac{1 + 1}{2} = \frac{2}{2} = 1
]
Adım 3: ( f(-1) )'i Bul
- ( x = -1 ) için, ( -1 < 0 ) olduğundan:
[
f(-1) = 1 - 3(-1) = 1 + 3 = 4
]
Sonuç Cevap
- Fonksiyonların toplamı:
[
f(3) + f(1) + f(-1) = 3 + 1 + 4 = 8
]
Bu tür parçalı fonksiyonlarda doğru aralığı seçmek kritiktir. @Sevin_Cicek