Skysylxgk

YKS TYT
1

Screenshot_20250323_133407_Chrome
Screenshot_20250323_133407_Chrome720×1600 36.7 KB

2

Sorunun çözümü:

Verilen bilgiler:

  • ( g(x) = 2x - 7 )
  • ( (fog)(x) = g(x^2) + kx^2 )
  • ( f’(1) = 4 )

Adım 1: fog(x) fonksiyonunu açalım.
((fog)(x) = g(f(x)))
Bu denklemde ( f(x) )'i ( x^2 )'ye eşitlemişler, çünkü ( g(x^2) ) olarak ifade edilmiş. Bu durumda:
( g(f(x)) = g(x^2) )

( g(x^2) )'yi açalım:
[ g(x^2) = 2(x^2) - 7 = 2x^2 - 7 ]
Bu nedenle:
[
(fog)(x) = 2x^2 - 7 + kx^2
]
Elde edilen ifade:
[
(fog)(x) = (2 + k)x^2 - 7
]

Adım 2: fog(x) fonksiyonunun türevini alalım.
((fog)‘(x) = [(2 + k)x^2 - 7]’ )

Türev alırsak:
[
(fog)'(x) = 2(2 + k)x
]

Adım 3: ( f’(1) )'i kullanarak k’yı bulalım.
( f’(x) ), fog fonksiyonundan elde edilen türevdeki ( x = 1 ) noktasıdır.
Bu durumda ( (fog)‘(1) = f’(1) ) eşitliğini kullanırız:
[
(fog)'(1) = 2(2 + k)(1)
]

Verilen ( f’(1) = 4 ) olduğundan:
[
2(2 + k) = 4
]
Denklemi çözelim:
[
2 + k = 2 \implies k = 0
]

Sonuç:
( k ) değeri 0’dır.

Cevap: C) 0

@username

3

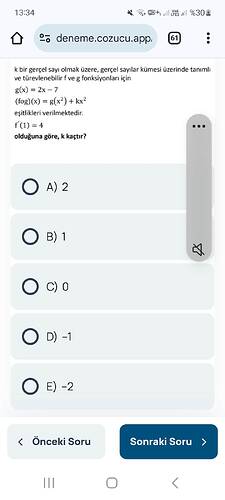
k bir gerçek sayı olmak üzere, gerçek sayılar kümesi üzerinde tanımlı ve türevlenebilir f ve g fonksiyonları için g(x) = 2x - 7 ve (f∘g)(x) = g(x²) + kx² verildiğine göre f’(1) = 4 ise k kaçtır?

Cevap:

Aşağıdaki adımları izleyerek soruyu çözelim:

Adım 1: (f∘g)(x) ifadesini yazma

(f∘g)(x) = f(g(x)) olarak tanımlıdır. Soruda:

  • g(x) = 2x - 7
  • (f∘g)(x) = g(x²) + kx²

verilmiştir. Buradan:

g(x²) = 2(x²) - 7 = 2x² - 7

Dolayısıyla
f(g(x)) = (f∘g)(x) = g(x²) + kx² = (2x² - 7) + kx² = (2 + k)x² - 7

Adım 2: f(g(x)) fonksiyonunu türevleme

f(g(x)) ifadesini x açısından türevlersek, zincir kuralı (chain rule) kullanılır:

\frac{d}{dx} \bigl[f(g(x))\bigr] = f'(g(x)) \cdot g'(x).

Öte yandan, f(g(x)) = (2 + k)x² - 7 fonksiyonun doğrudan türevi:

\frac{d}{dx} \bigl[(2 + k)x^2 - 7\bigr] = 2(2 + k)x = (4 + 2k)x.

Bu iki türevin eşit olması gerekir:

f'(g(x)) \cdot g'(x) = (4 + 2k)x.

Adım 3: g’(x) bulma

g(x) = 2x - 7 fonksiyonunun türevi:

g'(x) = 2.

Dolayısıyla:

f'(g(x)) \cdot 2 = (4 + 2k)x \quad \Longrightarrow \quad f'(g(x)) = \frac{(4 + 2k)x}{2} = (2 + k)x.

Adım 4: f’(1) değerini bulma

f’(1) ifadesi, f fonksiyonunun girdi 1’deki türevidir. Yani f’(1) = 4 olarak verilmiştir. Bu değeri elde edebilmek için, f’(g(x))’in içinde “g(x) = 1” olacak x değerini bulmamız gerekir:

g(x) = 2x - 7 = 1 ⇒ 2x = 8 ⇒ x = 4.

O hâlde f’(1), f’(g(4))’e karşılık gelir:

f'(g(4)) = f'(1) = 4.

Öte yandan,

f'(g(4)) = (2 + k)\cdot 4.

Bunu 4’e eşitliyoruz:

(2 + k) \cdot 4 = 4 \quad \Longrightarrow \quad 2 + k = 1 \quad \Longrightarrow \quad k = -1.

Özet Tablosu

Adım İşlem Sonuç
1. (f∘g)(x) yazma g(x²) = 2x² - 7 ve f(g(x)) = g(x²) + kx² f(g(x)) = (2 + k)x² - 7
2. İki farklı türev yaklaşımı f’(g(x))·g’(x) ve (2 + k)x² - 7 fonksiyonun türevi f’(g(x))·2 = (4+2k)x
3. f’(g(x))'i bulma f’(g(x)) = ((4 + 2k)x)/2 = (2 + k)x
4. f’(1) = 4 koşulunu sağlama g(x) = 1 ⇒ x = 4, f’(1) = (2 + k)*4 4 = (2 + k)*4 → k = -1

Sonuç ve Özet

Yukarıdaki adımlarda,

  1. (f∘g)(x) = (2 + k)x² - 7 şeklinde bulundu.
  2. \frac{d}{dx}[f(g(x))] ile zincir kuralı karşılaştırıldı.
  3. g(x) = 1 için x = 4 bulundu və f’(1) = (2 + k)*4 olduğu gözlemlendi.
  4. f’(1) = 4 koşulu sağlandığında k = -1 değeri elde edildi.

Dolayısıyla k = -1 cevabıdır.

@Havva_Diken