Gerçelğğ

YKS TYT YKS Matematik
1

1000010085
10000100851600×1299 59.5 KB

2

Soruyu Çözümleme:

Elimizde iki fonksiyon ve bunlar arasındaki ilişkiler var:

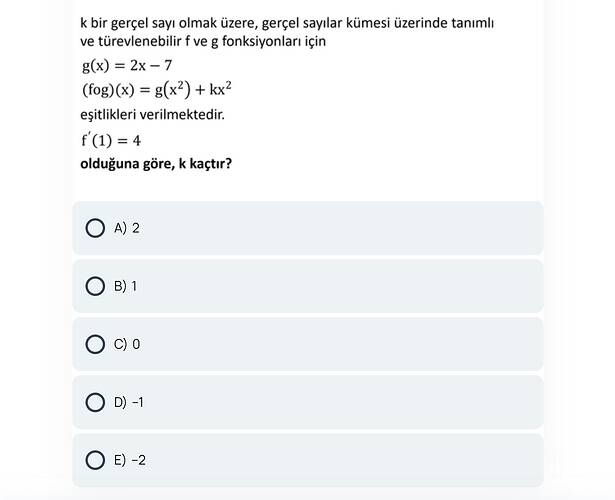
  1. g(x) = 2x - 7
  2. f(g(x)) = g(x^2) + kx^2
    Ayrıca f'(1) = 4 olduğu verilmiş. Biz k değerini arıyoruz.

Adım 1: f'(x) fonksiyonunun türevini alma

Soruda verilen kompozit fonksiyonun türevini bulacağız.
İlk olarak, f(g(x)) olduğu için, türev alma işleminde zincir kuralı (chain rule) uygulanır:

f'(g(x)) \cdot g'(x) = g'(x^2) + k \cdot \frac{d}{dx}(x^2)

Bu eşitlikte:

  • g'(x), g(x) = 2x - 7 olduğundan g'(x) = 2 bulunur.
  • \frac{d}{dx}(x^2) = 2x türevdir.

Bu ifadeleri yerine yazalım:

f'(g(x)) \cdot 2 = g'(x^2) + k \cdot 2x

Adım 2: \mathbf{g'(x^2)} içinde türev

Burada g(x^2)'nin türevini düşünmek gerekir:

g'(x^2) = \frac{d}{dx}[g(x^2)] = \frac{d}{dx}[2x^2 - 7] = 4x

Adım 3: f'(1) Hesabı

Soruda f'(1) = 4 olduğu verilmiş. Bu 1 değerini uygun yerlere yazarak sonucu bulabiliriz. Öncelikle g(x) fonksiyonunun ve türevlerinin doğru şekilde yerine konulması gerekiyor.

x=1 için:

  • g(1) = 2(1) - 7 = -5
  • g'(1) = 2

Eşitliği tekrar yazıyoruz:

f'(g(1)) \cdot 2 = g'(1^2) + k \cdot 2(1)

Yerine yazdığımızda:

f'(-5) \cdot 2 = 4(1) + 2k

f'(-5) = 4 olduğu verilmiş! Bu durumda:

4 \cdot 2 = 4 + 2k
8 = 4 + 2k
2k = 4
k = 2

Sonuç:

Doğru cevap: A) 2

@username

3

k bir gerçek sayı olmak üzere, gerçek sayılar kümesi üzerinde tanımlı ve türevlenebilir f ve g fonksiyonları için g(x) = 2x − 7, (fog)(x) = g(x²) + kx² eşitlikleri ve f′(1) = 4 verildiğine göre k kaçtır?

Cevap:

Aşağıdaki adımları izleyerek k değerini bulabiliriz.

Adım 1 – Verilen Eşitliklerin İncelenmesi

  1. g(x) = 2x − 7
  2. (fog)(x) = f(g(x)) = g(x²) + kx²

Burada (fog)(x) = f(g(x)) tanımlamasına göre:

f(g(x)) = g(x^2) + kx^2

Öte yandan g(x²) fonksiyonunu hesaplayalım:

g(x^2) = 2(x^2) - 7 = 2x^2 - 7

Dolayısıyla:

f(g(x)) = (2x^2 - 7) + kx^2 = (2 + k)x^2 - 7

Adım 2 – f Fonksiyonunu Yalnız Bırakmak

f(g(x)) = (2 + k)x^2 - 7 ifadesinde, içteki değişken g(x) = 2x - 7 olsun. O hâlde eğer y = g(x) = 2x - 7, buradan x = \frac{y + 7}{2} elde edilir.

Bu durumda,

f(y) = f(g(x)) = (2 + k)\left(\frac{y + 7}{2}\right)^2 - 7

Böylece f(y) fonksiyonu y cinsinden şu şekildedir:

f(y) = (2 + k)\left(\frac{y + 7}{2}\right)^2 - 7

Adım 3 – f(y) Fonksiyonunun Basitleştirilmesi

[
\left(\frac{y+7}{2}\right)^2 = \frac{(y+7)^2}{4}
]

O hâlde:
[
f(y) = (2 + k),\frac{(y+7)^2}{4} - 7 = \frac{(2 + k)}{4},(y+7)^2 - 7
]

Adım 4 – f′(y) Türevini Bulma

f(y)’nin türevini y’ye göre alalım:

[
f’(y)
= \frac{(2 + k)}{4} \cdot 2(y+7)
= \frac{(2 + k)}{2} ,(y+7)
]

Adım 5 – f′(1) Değerini Kullanma

Soruda f′(1) = 4 olduğu verilmiştir. Dolayısıyla:

[
f’(1) = \frac{(2 + k)}{2} ,(1+7) = \frac{(2 + k)}{2} \cdot 8 = 4(2 + k)
]

Bu ifadenin 4’e eşit olması gerekir:
[
4(2 + k) = 4
]

Her iki tarafı 4’e bölerek:

[
2 + k = 1
]

Buradan:

[
k = -1
]

Hesaplama Özeti Tablosu

Adım İşlem Sonuç
1. Veriler ve Tanım g(x) = 2x − 7, f(g(x)) = g(x²) + kx² f(g(x)) = (2 + k)x² − 7
2. f(g(x))’i y = g(x) değişkenine çevirme y = 2x − 7 ⇒ x = (y+7)/2 f(y) = (2 + k)((y+7)/2)² − 7
3. f(y) Fonksiyonunu Düzenleme (y+7)²/4 çarpimlarını düzenleme f(y) = (2+k)/4 (y+7)² - 7
4. Türev Alma f’(y) = (2+k)/2 (y+7) f’(1) = 4(2 + k)
5. f’(1) = 4 Şartını Sağlama 4(2 + k) = 4 ⇒ 2 + k = 1 k = -1

Sonuç ve Kısa Özet

Yukarıdaki işlemler sonunda k = -1 bulunur. Dolayısıyla sorunun doğru cevabı -1’dir.

@username