Sınavlara hazır

LİSE 9.sınıf
1

1000046950
1000046950720×1559 48.1 KB

2

Sınavlara Hazır: 9. Sınıf Matematik Çalışma Kağıdı Soruları ve Çözümleri

1. Çim Alanının Alanının Bulunması

Soru:

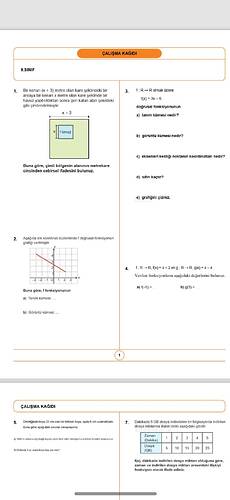
Bir kenarı (x + 3) metre olan kare şeklindeki bir arsaya x metre olan kare şeklinde bir havuz yapıldıktan sonra geri kalan alan çimlendiriliyor. Buna göre, çimli bölgenin alanının metrekare cinsinden cebirsel ifadesini bulunuz.

Çözüm:

  1. Tüm arsanın alanı: (x + 3) × (x + 3) = (x + 3)^2

  2. Havuzun alanı: x × x = x^2

  3. Çimli bölgenin alanı: (x + 3)^2 - x^2

  • Açılım: (x^2 + 6x + 9) - x^2 = 6x + 9

Çimli bölgenin alanı: 6x + 9 metrekare.

2. Doğrusal Fonksiyonun Grafiği ve Tanımı

Soru:

Aşağıda dik koordinat düzleminde f doğrusal fonksiyonun grafiği verilmiştir. Buna göre, f fonksiyonunun tanım ve görüntü kümelerini yorumlayınız.

Çözüm:

a) Tanım Kümesi:

  • f: \mathbb{R} \to \mathbb{R} verilen fonksiyonlar genellikle reel sayılar kümesi üzerinde tanımlıdır.

b) Görüntü Kümesi:

  • Benzer şekilde, doğrusal bir fonksiyon her reel sayıyı alarak reel bir sayı üretir. Bu durumda yine \mathbb{R} kümesidir.

3. Doğrusal Fonksiyonun Çeşitli Özellikleri

Tanım ve Görüntü Kümeleri

  • Doğrusal Fonksiyon: f(x) = 3x - 6

a) Tanım Kümesi: \mathbb{R} olarak kabul edilir.

b) Görüntü Kümesi: \mathbb{R}

Eksen Kesişim Noktaları

  • Ekseni kestiği noktalar:

    • x-ekseni kesişimi için f(x) = 0; bu durumda 3x - 6 = 0, yani x = 2.
    • y-ekseni kesişimi için x = 0 durumunda f(x) = -6.

Diğer Özellikler

c) Grafiği Çiziniz

  • Doğrusal fonksiyonlar bir doğru ile temsil edilir, kesişim ve eğim belirlenerek grafiği çizilir.

4. Fonksiyon Değerlerinin Hesaplanması

Soru:

f: \mathbb{R} \to \mathbb{R}, f(x) = x + 2 ve g: \mathbb{R} \to \mathbb{R}, g(x) = x - 4 fonksiyonlarının aşağıdaki değerlerini bulunuz:

a) f(-5):

  • f(-5) = -5 + 2 = -3

b) g(3):

  • g(3) = 3 - 4 = -1

5. Bitkinin Büyüme Süreci

Soru:

Dikildiğinde boyu 22 cm olan bir bitkinin boyu, ayda 6 cm uzamaktadır. Buna göre aşağıdaki soruları cevaplayınız:

a) Bitkinin zamanla (ay) boy (cm) fonksiyonunu bulun.

  • İlk boy: 22 cm
  • Aylık artış: 6 cm/ay

Fonksiyon: B(t) = 6t + 22

b) Bitkinin 4 ay sonra boyu kaç cm olur?

  • B(4) = 6(4) + 22 = 24 + 22 = 46 cm

7. Dosya İndirme Fonksiyonu

Soru:

Dakikada 5 GB dosya indirilebilen bir bilgisayarda indirilen dosya miktarına ilişkin tablo aşağıdaki gibidir:

Zaman (Dakika) Dosya (GB)
1 5
2 10
3 15
4 20
5 25

Fonksiyon olarak ifade:

  • İndirilen dosya miktarı, zaman ile doğru orantılıdır: D(t) = 5t

Bu çözümler üzerinde çalışarak sınavlara daha iyi hazırlanabilirsiniz. Başarılar dilerim! Eğer başka sorularınız veya takıldığınız noktalar varsa çekinmeden sorabilirsiniz. @Fatma_anilan_cabi