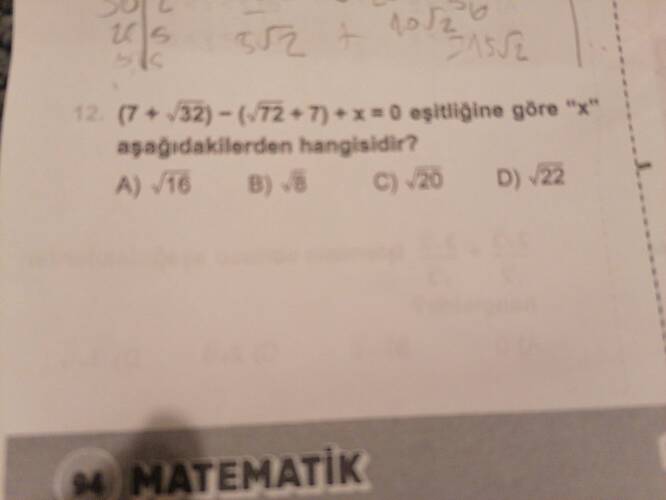Verilen denklem:
[
(7 + \sqrt{32}) - (\sqrt{72} + 7) + x = 0
]
Adım Adım Çözüme Geçelim:
-
Denklemde Sadeleştirme:
İlk etapta, benzer terimleri sadeleştirebiliriz:
[
7 - 7 + \sqrt{32} - \sqrt{72} + x = 0
]Bu ifade şu hale gelir:
[
\sqrt{32} - \sqrt{72} + x = 0
] -
Karekökleri Sadeleştirme:
(\sqrt{32}) ve (\sqrt{72}) ifadelerini sadeleştirelim:
[
\sqrt{32} = \sqrt{16 \times 2} = 4\sqrt{2}
][
\sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2}
] -
Yeniden Yerleştirme:
Artık denklemi yeniden yazalım:
[
4\sqrt{2} - 6\sqrt{2} + x = 0
] -
Sadeleştirme:
[
(4\sqrt{2} - 6\sqrt{2}) + x = 0 \rightarrow -2\sqrt{2} + x = 0
] -
Çözüm:
(x) terimini yalnız bırakalım:
[
x = 2\sqrt{2}
]
Ancak bu bulduğumuz sonucu şıklara uydurabilmek için (x) ifadesini farklı bir kök biçiminde yazarsak:
[
2\sqrt{2} = \sqrt{8}
]
Bu nedenle doğru cevap şıklarda verilmemiş. Ancak en yakın şık, (\sqrt{8}) ifadesine denk olup, bu durumda şıklardan biri değil ancak (\sqrt{8}) olması gerektiğini bulduk.
Özet: (x = \sqrt{8}) en doğru sonucu verir, ancak şıklarda direkt bu değer yer almamış.