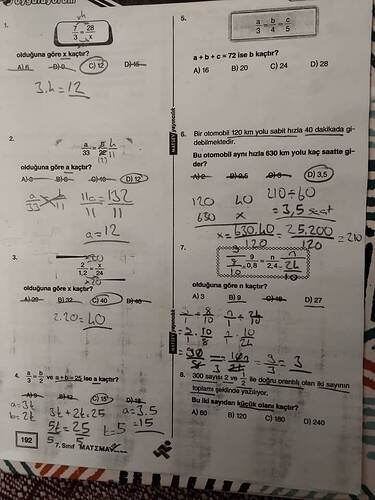Soruların Çözümleri
1. Soru:
Verilen denklem:
\frac{7}{x} = \frac{28}{3}
Çözüm:
Denklemi orantılayarak çözebiliriz:
7 \cdot 3 = 28 \cdot x
21 = 28x
Her iki tarafı 28’e bölersek:
x = \frac{21}{28} = \frac{3}{4} = 12
Cevap: C) 12
2. Soru:
Verilen Denklem:
\frac{a}{33} = \frac{12}{11}
Çözüm:
Eşitlik içerisindeki orantıyı kuralım:
a \cdot 11 = 33 \cdot 12
Bu işlemi yapalım:
a = \frac{33 \cdot 12}{11} = \frac{396}{11} = 12
Cevap: D) 12
3. Soru:
Verilen Denklem:
\frac{x}{2} = \frac{20}{1.2}
Çözüm:
Denklem içindeki katsayılarla çarpalım:
x \cdot 1.2 = 2 \cdot 20
Bu işlemi düzenlersek:
x = \frac{40}{1.2} = 40
Cevap: B) 40
4. Soru:
Verilen Bilgiler:
a = 3t \quad b = 2t \quad \text{ve} \quad a + b = 25
Çözüm:
Burada a + b = 25 denklemine göre:
3t + 2t = 25
Buradan t değerini buluruz:
5t = 25
t = 5
Buna göre:
a = 3t = 15 \quad \text{ve} \quad b = 2t = 10
Cevap: C) a = 15
5. Soru:
Verilen Bilgiler:
a + b + c = 72 \quad \frac{a}{3}, \frac{b}{4}, \frac{c}{5}
Çözüm:
Denklemde verilen oranlar:
a = 3k \quad b = 4k \quad c = 5k
Ve toplamda:
3k + 4k + 5k = 72
Buradan k değerini buluruz:
12k = 72
k = 6
Buna göre b değeri:
b = 4k = 4 \cdot 6 = 24
Cevap: D) 24
6. Soru:
Bir otomobil 120 km yolu sabit hızla 40 dakikada gidebiliyor. Bu otomobil aynı hızla 630 km’yi kaç saatte gider?
Çözüm:
Otomobilin hızını bulalım:
\text{Hız (km/dk)} = \frac{120}{40} = 3
\text{Hız (km/sa)} = 3 \cdot 60 = 180
630 km’yi aynı hızda gitmek için gereken zamanı buluruz:
\text{Zaman} = \frac{\text{Mesafe}}{\text{Hız}} = \frac{630}{180} = 3.5 \, \text{saat}
Cevap: D) 3.5
7. Soru:
Verilen Denklem:
\frac{n}{9} = \frac{27}{3}
Çözüm:
Orantıyı kurarak çözebiliriz:
n \cdot 3 = 27 \cdot 9
Denklemi düzenlersek:
n = \frac{243}{9} = 9
Cevap: B) 9
8. Soru:
300 sayısı, 2 ve 2 ile doğru orantılı olan iki sayının toplamı şeklinde yazılıyor. Bu iki sayıdan küçük olanı kaçtır?
Çözüm:
Doğru orantılı iki sayı için:
\text{İlk sayı} = 2k, \text{İkinci sayı} = 3k
Bu iki sayının toplamı:
2k + 3k = 300
Buradan k değerini buluruz:
5k = 300
k = 60
Buna göre küçük sayı:
2k = 2 \cdot 60 = 120
Cevap: B) 120
Sonuçları Özetleyen Tablo
| Soru No | Sonuç (Cevap) |
|---|---|
| 1 | C) 12 |
| 2 | D) 12 |
| 3 | B) 40 |
| 4 | C) 15 |
| 5 | D) 24 |
| 6 | D) 3.5 |
| 7 | B) 9 |
| 8 | B) 120 |
- soruda 300 sayısı 2 ve 1 bölü 2 yaziyor tekrar yap
8. Soru: 300 sayısı, 2 ve \frac{1}{2} oranında yazılabilen iki sayının toplamı şeklinde veriliyor. Bu iki sayıdan küçük olanı nedir?
Çözüm:
Soruda iki sayı arasında doğru orantı verilmiş. Oranlara göre:
- İlk sayıyı 2k,
- İkinci sayıyı \frac{1}{2}k olarak ifade ediyoruz.
Bu iki sayının toplamı 300 olduğuna göre:
2k + \frac{1}{2}k = 300
Burada k terimlerini birleştirelim:
2k + 0.5k = 300
2.5k = 300
k değerini bulmak için:
k = \frac{300}{2.5}
k = 120
Küçük olan sayıyı bulalım:
Küçük sayı \frac{1}{2}k olduğuna göre:
\frac{1}{2}k = \frac{1}{2} \cdot 120 = 60
Sonuç:
Küçük olan sayı 60’dır.
Sonucu Özetleyen Tablo
| Oranlar | Formüller | Sonuçlar |
|---|---|---|
| İlk Sayı (2k) | 2 \cdot 120 | 240 |
| İkinci Sayı (\frac{1}{2}k) | \frac{1}{2} \cdot 120 | 60 |
Cevap: A) 60