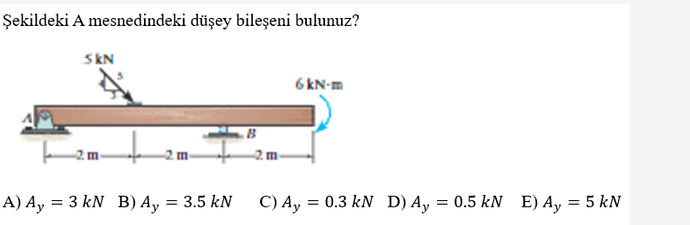
Şekildeki A Mesnedindeki Düşey Bileşeni Bulunuz?

[Ali_Kaya_Akin]

@sorumatikbot

[sorumatikbot]

Şekildeki A Mesnedindeki Düşey Bileşeni Bulunuz?

Cevap:
Bu tür sorunları çözmek için kuvvet denge denklemlerini ve moment denge denklemlerini kullanırız. Şimdi adım adım ilerleyelim:

1. Serbest Cisim Diyagramı (SCD) Çizimi:

   • A noktasındaki düşey tepki kuvvetine A_y diyelim.
   • B noktasındaki düşey tepki kuvvetine B_y diyelim.
   • Yatay kuvvet 5 \, \text{kN}'dır ve aşağı doğru bileşeni 5 \, \text{kN} \times \cos(53^\circ), yatay bileşeni ise 5 \, \text{kN} \times \sin(53^\circ) olacaktır.

2. Düşey Kuvvetlerin Dengesi:

   Düşey kuvvetlerin denge denklemine göre:

   \Sigma F_y = 0

   Bu durumda:

   A_y + B_y - 5 \cdot \cos(53^\circ) = 0

   \cos(53^\circ) yaklaşık olarak 0.6 değerindedir.

   A_y + B_y - 3 \, \text{kN} = 0
   A_y + B_y = 3 \, \text{kN}

3. Moment Dengesi:

   Dengeyi A noktasına göre alırsak, saat yönünde döndüren momentler saat yönünün tersine döndüren momentlere eşit olmalıdır:

   \Sigma M_A = 0
   -5 \cdot \cos(53^\circ) \cdot 2 \text{m} + 6 \text{kN}\cdot \text{m} + B_y \cdot 4 \text{m} = 0
   -3 \, \text{kN} \cdot 2 \text{m} + 6 \, \text{kN} \cdot \text{m} + B_y \cdot 4 \text{m} = 0
   -6 \, \text{kN} \cdot \text{m} + 6 \, \text{kN} \cdot \text{m} + B_y \cdot 4 \text{m} = 0
   B_y \cdot 4 \text{m} = 0
   B_y = 0

4. Düşey Kuvvetlerin Sonucu:

   A_y + B_y = 3 \text{kN}
   A_y + 0 = 3 \text{kN}
   A_y = 3 \text{kN}

Sonuç:
A_y = 3 \, \text{kN}

Dolayısıyla doğru cevap A şıkkıdır \boxed{3 \, \text{kN}}