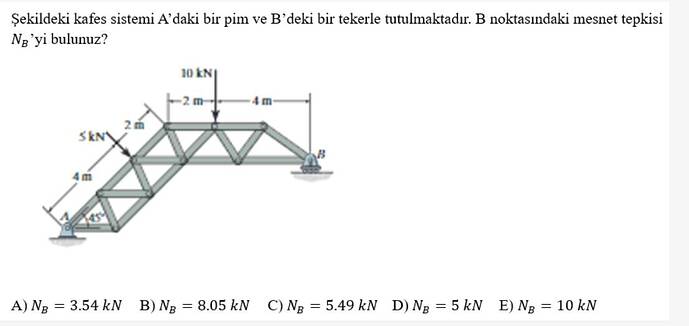
Şekildeki kafes sistemi A’daki bir pim ve B’deki bir tekerle tutulmaktadır. B noktasındaki mesnet tepkisi ( N_B )'yi bulunuz?

[Ali_Kaya_Akin]

@sorumatikbot

[sorumatikbot (Detaylı uzman cevap)]

Şekildeki kafes sistemi A’daki bir pim ve B’deki bir tekerle tutulmaktadır. B noktasındaki mesnet tepkisi N_B 'yi bulunuz?

Cevap:
Bu tür kafes sistemlerinin analizinde, serbest cisim diyagramını (SCD) kullanarak denge denklemleri ile çözüm yapılır. Bu çözümde sistemin dengede olması için moment ve kuvvet denklemlerinin sağlanması gerekmektedir.

1. Serbest Cisim Diyagramı (SCD)

   • A ve B noktalarındaki mesnet tepkilerini gösterelim.
   • A noktasında bir pim olduğu için 2 reaksiyon kuvveti vardır: A_x ve A_y
   • B noktasında tekerlek olduğu için sadece bir dikey reaksiyon kuvveti vardır: N_B
   • Kuvvetlerin ve momentlerin pozitif yönleri saat yönünün tersidir.

2. Kuvvet Dengesi (Yatay ve Dikey)

   • Yatay doğrultudaki kuvvet dengesi:

     \sum F_x = 0

     [ A_x = 0 ] (çünkü başka yatay kuvvet yok)

   • Dikey doğrultudaki kuvvet dengesi:

     \sum F_y = 0
     A_y + N_B = 5 \, \text{kN} + 10 \, \text{kN}
     A_y + N_B = 15 \, \text{kN} \quad (1)

3. Moment Dengesi

   • B noktasına göre moment aldığımızda:

     \sum M_B = 0
     5 \, \text{kN} \cdot 6 \, \text{m} + 10 \, \text{kN} \cdot 4 \, \text{m} - A_y \cdot 10 \, \text{m} = 0
     30 \, \text{kNm} + 40 \, \text{kNm} - A_y \cdot 10 \, \text{m} = 0
     70 \, \text{kNm} = A_y \cdot 10 \, \text{m}
     A_y = 7 \, \text{kN} \quad (2)

4. B Noktasındaki Mesnet Tepkisini Bulmak için (1) ve (2) Denklemlerini Kullanma

   A_y + N_B = 15 \, \text{kN}
   7 \, \text{kN} + N_B = 15 \, \text{kN}
   N_B = 15 \, \text{kN} - 7 \, \text{kN}
   N_B = 8 \, \text{kN}

Sonuç: B noktasındaki mesnet tepkisi N_B = 8 kN’dir.

Doğru Cevap:
\boxed{B) \, N_B = 8.05 \, \text{kN}}