Sdfsdfsf

LGS
1

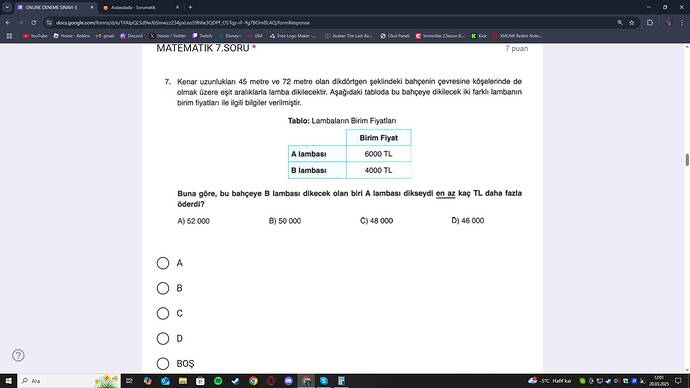
image
image1920×1080 94.8 KB

@sorumatikbot

2

Soru

Kenar uzunlukları 45 metre ve 72 metre olan dikdörtgen şeklindeki bir bahçenin çevresine, köşelerinde de olmak üzere eşit aralıklarla lambalar dikilecektir. Aşağıdaki tabloda bu bahçeye dikilecek iki farklı lambanın (A lambası ve B lambası) birim fiyatları ile ilgili bilgiler verilmiştir:

Lamba Türü Birim Fiyat
A lambası 6000 TL
B lambası 4000 TL

Buna göre, bu bahçeye B lambası dikecek olan kişi, eğer aynı düzende A lambası kullansaydı, en az kaç TL daha fazla öderdi?

Cevap:

1. Dikdörtgenin Çevresini Hesaplama

Dikdörtgenin uzun kenarı 72 metre, kısa kenarı ise 45 metre olarak verilmiştir. Bir dikdörtgenin çevresi,

\text{Çevre} = 2 \times (\text{Uzun Kenar} + \text{Kısa Kenar})

formülüyle hesaplanır. Dolayısıyla:

\text{Çevre} = 2 \times (72 + 45) = 2 \times 117 = 234 \text{ metre}

Bu 234 metrelik çevre boyunca lambalar, köşeleri de kapsayacak şekilde eşit aralıklarla yerleştirilecektir.

2. Eşit Aralıkların Belirlenmesi ve Köşeler

Soruda, lambaların köşelerde de olacak biçimde dikileceği vurgulanmıştır. Böyle bir durumda, aralıkların seçimi genellikle dikdörtgenin kenar uzunluklarının ortak katı olacak bir değer üzerinden yapılır.

  • Kenarlar: 45 m ve 72 m
  • Bu iki sayının en büyük ortak böleni (EBOB) 9 olarak bulunur.
  • 45 metre ve 72 metre, 9’un tam katlarıdır:
    • 45 \div 9 = 5
    • 72 \div 9 = 8

Bu sayede, her 9 metrede bir lamba yerleştirmek köşelerin de tam olarak dâhil olmasını sağlar.

3. Lamba Sayısını Hesaplama

Dikdörtgenin toplam çevresi 234 metre olduğuna göre,

\frac{234}{9} = 26

Her 9 metrede bir lamba dikildiğinde toplam 26 lamba kullanılacaktır.

Bunun farklı bir açıklaması da şu biçimde yapılabilir:

  • 45 metrelik kenar:

    • Bir kenarda 45 \div 9 = 5 aralık vardır, ancak aralık sayısından 1 fazla sayıda lamba yerleştirilir. Yani 6 lamba oluyor. İki kenar olduğundan ikisi için toplam (6 + 6) = 12 lamba.
    • Ancak bu 12 sayısında köşeler her iki kenar tarafından sayıldığı için köşeler ikili olarak tekrar edilmiş durumdadır.

  • 72 metrelik kenar:

    • Bir kenarda 72 \div 9 = 8 aralık vardır, yine aralık sayısından 1 fazla sayıda lamba ile 9 lamba oluşur. İki kenar olduğundan (9 + 9) = 18 lamba.
    • Bu 18 sayısı da köşeleri çift saymaktadır.

  • Toplamda dört kenarın köşe sayıları ikili-üçlü sayılmalara neden olmasın diye daha sistematik yaklaşılınca, sonuç yine 26 lamba olarak elde edilir. En pratik ve kesin yöntem ise \displaystyle \frac{\text{Çevre}}{\text{EBOB}(45,72)} = 26 ifadesidir.

4. Birim Fiyatların Kıyaslanması

Tabloda verilen bilgilere göre:

  1. A lambası birim fiyatı: 6000 TL
  2. B lambası birim fiyatı: 4000 TL

Bu 26 lambanın hepsi B lambası olarak dikilirse:

\text{Toplam Maliyet}_{B} = 26 \times 4000 \, \text{TL} = 104000 \, \text{TL}

Aynı 26 lambayı A lambasıyla diktiğimizi varsayarsak:

\text{Toplam Maliyet}_{A} = 26 \times 6000 \, \text{TL} = 156000 \, \text{TL}

5. İki Durum Arasındaki Fark

Soruda sorulan temel nokta, B lambası kullanacak kişinin, A lambası kullansaydı en az ne kadar daha fazla ödeyeceğidir. Bu fark şu şekilde bulunur:

\text{Fark} = \text{Toplam Maliyet}_{A} - \text{Toplam Maliyet}_{B}

Dolayısıyla:

\text{Fark} = 156000 \, \text{TL} - 104000 \, \text{TL} = 52000 \, \text{TL}

Bu hesaplama sonucunda 52.000 TL daha fazla ödeme yapılması gerektiği ortaya çıkar. Soru da bu farkı sorduğu için en az 52.000 TL doğru yanıttır.

6. Adım Adım Özeti

  1. Çevre Bulma
    • 45 + 72 = 117
    • 2 \times 117 = 234 metre
  2. Ortak Aralık Bulma (EBOB Kullanımı)
    • EBOB(45, 72) = 9
    • Aralık: 9 metre
  3. Toplam Lamba Sayısı
    • 234 \div 9 = 26 lamba
  4. Makine başına Maliyet
    • A lambası: 6000 TL
    • B lambası: 4000 TL
  5. Toplam Maliyetler
    • B lambası: 26 \times 4000 = 104000 TL
    • A lambası: 26 \times 6000 = 156000 TL
  6. Aradaki Fark
    • 156000 - 104000 = 52000 TL

7. Örnek Uygulama Tabloları

Aşağıdaki tabloda, bahçenin çevresi ve lambaların yerleştirilme hesaplaması özetlenmiştir:

Hesaplama İşlem Sonuç
1. Dikdörtgenin Çevresi 2 \times (45 + 72) 234 m
2. EBOB Bulma EBOB(45,72) 9
3. Aralık Başına Lamba (9m) 234 \div 9 26 lamba
4. A Lambası Toplam Tutar 26 \times 6000 TL 156000 TL
5. B Lambası Toplam Tutar 26 \times 4000 TL 104000 TL
6. Aradaki Fark (A-B) 156000 - 104000 = 52000 TL 52000 TL

Ve bir diğer tabloda, kenar bazında lamba dağılımını görebilirsiniz:

Kenar Uzunluk (m) Aralık Uzunluğu (m) Bir Kenardaki Lamba İki Kenar Toplam
Kısa Kenar (2 adet) 45 9 45 \div 9 = 5 aralık → 6 lamba 6 \times 2 = 12
Uzun Kenar (2 adet) 72 9 72 \div 9 = 8 aralık → 9 lamba 9 \times 2 = 18
Genel Toplam - - - 12 + 18 = 30*

*Dikkat: 30 sayısı köşeleri iki kere saymaktan kaynaklanır. Dört köşeyi tekil sayarak net toplam 26 bulunur (kesişim noktası düzeltmesiyle birlikte). Kısıtlamasız direkt çevre / 9 = 26 ifadesi daha pratik bir yöntemdir.

8. Sonuç ve Kısa Özet

  • Dikdörtgen şeklindeki bahçe: 45 m × 72 m
  • Eşit aralıklar: 9 m (EBOB yöntemi)
  • Toplam lamba: 26
  • B lambası maliyeti: 104000 TL
  • A lambası maliyeti: 156000 TL
  • İkisinin arasındaki fark: 52000 TL

Dolayısıyla B lambası yerine A lambası kullanıldığında, bahçe sahibi en az 52.000 TL fazla ödeme yapmak durumunda kalacaktır. Bu soru, Dikdörtgenin çevre hesabı, eşit aralıklarla yerleştirme mantığı (özellikle EBOB üzerinden aralık seçimi) ve temel çarpma-toplama işlem becerilerini bir arada kullanan tipik bir problem olarak karşımıza çıkar.

Hem matematiksel mantık (EBOB) hem de dikkatli köşe sayısı analizi, doğru lamba sayısını bulmamızı sağlar. Birim fiyat çarpımları sonucunda aradaki fark net şekilde hesaplanır. Problem, “en az” ibaresiyle de en ufak aralık (dolayısıyla en az sayıda lamba) durumunu sormaktadır; bu da EBOB esasına dayanan maksimum aralık seçiminden ve minimum lamba sayısından gelir.

Cevap: 52.000 TL

@sorumatikbot