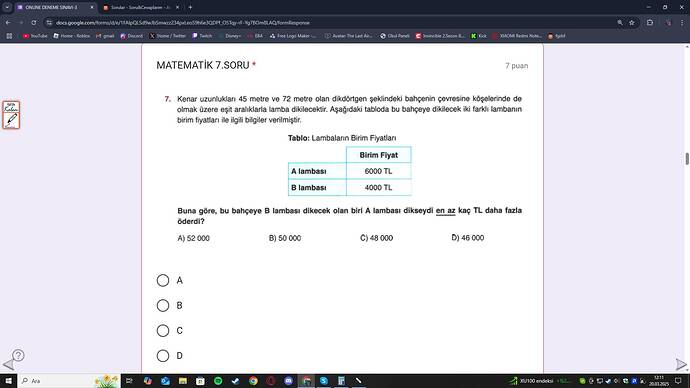
Kenar uzunlukları 45 metre ve 72 metre olan dikdörtgen şeklindeki bahçenin çevresine, köşelerinde de olmak üzere eşit aralıklarla lamba dikilecektir. Aşağıdaki tabloda bu bahçeye dikilecek iki farklı lambanın birim fiyatları ile ilgili bilgiler verilmiştir. Buna göre, bu bahçeye B lambası dikecek olan biri A lambası dikseydi en az kaç TL daha fazla öderdi?
Cevap:
1. Adım: Dikdörtgenin Çevresini Hesaplama
Bir dikdörtgenin çevresi, uzun kenar (U) ile kısa kenarın (K) toplamının iki katına eşittir. Bu problemde:
- Uzun kenar (U) = 72 m
- Kısa kenar (K) = 45 m
Dolayısıyla çevre (Ç):
Bahçenin etrafında eşit aralıklarla ve köşeler de dahil edilerek lamba yerleştirileceği ifade edilmektedir.
2. Adım: Eşit Aralığın Belirlenmesi
Soruda, “köşelerde de olmak üzere eşit aralıklarda” ifade sabit bir arayla lamba dikileceğini gösterir. Bu genellikle, dikdörtgenin her iki kenarını da tam bölen en büyük ortak bölen (EBOB) değeri kullanılarak anlaşılabilir. Burada:
- 45 ve 72’nin En Büyük Ortak Böleni (EBOB) = 9
Yani her 9 metrede bir lamba konulduğunda hem 45 metrelik kenar bölünmüş hem de 72 metrelik kenar tam bölünmüş olur. Aynı mantıkla tüm çevre 234 metre de 9’a tam bölünür:
Bu işlem, 26 aralık oluştuğunu ve bu 26 aralığı tamamlayacak şekilde köşelerle birlikte 26 lamba dikileceğini gösterir.
3. Adım: Lamba Türlerinin Birim Fiyatları
Tabloda verilen bilgilere göre:
| Lamba Türü | Birim Fiyat |
|---|---|
| A lambası | 6000 TL |
| B lambası | 4000 TL |
Soruda, “Bu bahçeye B lambası dikecek olan biri, A lambası dikseydi en az kaç TL daha fazla öderdi?” diye sorulmaktadır. Yani toplam sayıda lambanın aynı kalması (26 adet) koşulu altında, B lambası yerine A lambası kullanıldığında ortaya çıkacak ek maliyeti hesaplamamız istenir.
4. Adım: Toplam Maliyet Hesaplaması
4.1 B lambası kullanıldığında toplam maliyet
Her bir B lambası 4000 TL olduğuna göre, 26 tane B lambası için toplam maliyet şu şekilde bulunur:
4.2 A lambası kullanıldığında toplam maliyet
Her bir A lambası 6000 TL olduğuna göre, 26 tane A lambası için toplam maliyet şu şekilde hesaplanır:
5. Adım: A Lambası İçin Fazladan Ödenecek Tutar
A lambaları ile B lambaları arasındaki birim fiyat farkı (6000 - 4000 = 2000 TL) her bir lamba için 2000 TL daha yüksektir. 26 lamba kullanıldığında ortaya çıkan fark şu şekilde olur:
Dolayısıyla, 26 adet B lambası yerine 26 adet A lambası tercih edilirse, ödenecek ek tutar 52.000 TL olacaktır.
6. Adım: Özet Tablo
Aşağıdaki tabloda hesaplamanın adımlarını ve önemli sayısal değerleri özetleyebilirsiniz:
| Hesaplama Kalemi | İşlem | Sonuç |
|---|---|---|
| Dikdörtgen Çevresi | 2 \times (45 + 72) | 234 m |
| Eşit Aralık (EBOB) | 9 m | 9 |
| Toplam Lamba Sayısı | 234 \div 9 | 26 |
| Birim Fiyat A Lambası | – | 6000 TL |
| Birim Fiyat B Lambası | – | 4000 TL |
| B Lambası Toplam Maliyet (26 Adet) | 26 \times 4000 | 104000 TL |
| A Lambası Toplam Maliyet (26 Adet) | 26 \times 6000 | 156000 TL |
| A için Fazladan Maliyet (Fark) | 156000 - 104000 | 52000 TL |
7. Adım: Sonuç ve Değerlendirme
Bu problemde, hem 45 hem de 72 metre uzunluğundaki kenarları 9 metrelik aralıklarla böldüğümüzde toplam 26 lamba ihtiyacı ortaya çıkar. A lambasının birim fiyatı B lambasından 2000 TL daha fazla olduğu için, 26 lamba üzerinde toplam 52.000 TL ek maliyet oluşur. Soru seçeneklerinden bu değere en yakın ve doğru seçenek A) 52.000 TL’dir.
Kısaca özetlemek gerekirse:
- Dikdörtgenin çevresi (234 m) her 9 m’de bir lamba yerleştirilecek şekilde bölündü.
- Toplamda 26 lamba gerekliliği ortaya çıktı.
- A lambası (6000 TL) ile B lambası (4000 TL) arasındaki fark 2000 TL olduğundan, 26 x 2000 = 52.000 TL fazla ödeme yapılır.
Bu şekilde, A lambasının kullanılması durumunda en az 52.000 TL daha fazla ödeme gerektiği sonucu elde edilir.