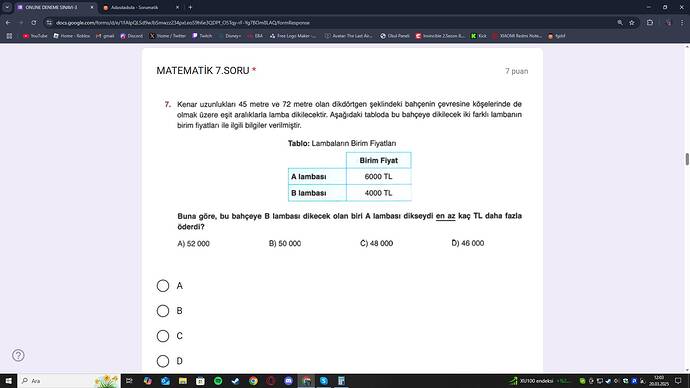
Soru: Kenar uzunlukları 45 metre ve 72 metre olan dikdörtgen şeklindeki bahçenin çevresine, köşelerinde de olmak üzere eşit aralıklarla lamba dikilecektir. Aşağıdaki tabloda bahçeye dikilecek iki farklı lambanın birim fiyatları yer almaktadır. Buna göre, bu bahçeye B lambası dikecek olan biri A lambası dikseydi en az kaç TL daha fazla öderdi?
| Lambaların Birim Fiyatları | Birim Fiyat |
|---|---|
| A lambası | 6000 TL |
| B lambası | 4000 TL |
A) 52 000
B) 50 000
C) 48 000
D) 46 000
Answer:
1. Sorunun Analizi
Bu problemde, dikdörtgen şeklindeki bir bahçenin tüm köşelerine ve kenarlarına eşit aralıklarla lamba yerleştirilecektir. Eşit aralık kuralı bahçenin çevresindeki tüm lambalar arasında aynı mesafe olmasını ve aynı zamanda köşelere de lamba dikilmesini şart koşar. İki tip lamba vardır: A lambası (birim fiyatı 6000 TL) ve B lambası (birim fiyatı 4000 TL). Soru bize, aslında B lambası kullanan bir kişinin, eğer A lambası kullansaydı, en az ne kadar fazla ödeme yapacağını sorar.
Burada “en az” ibaresi önemlidir; çünkü en fazla aralık (yani en büyük mesafe) kullanılarak lambaların sayısı minimize edilir ve bu şekilde iki lamba seçeneği arasındaki fiyat farkı da minimize edilmiş olur. Dolayısıyla kurulum masrafları arasındaki farkı hesaplayabilmek için, önce tek tip lambayla yapılacak doğru kurulumda kaç lamba dikileceğini bulmamız gerekir.
2. Bahçenin Çevresi
Dikdörtgenin kısa kenarı 45 metre, uzun kenarı 72 metre’dir.
Bahçenin toplam çevresi şu şekilde hesaplanır:
Bu değeri hesaplayalım:
- Kısa kenar + uzun kenar = 45 + 72 = 117
- Çevre = 2 × 117 = 234 metre
3. Lambaların Yerleştirilmesi
Lambalar köşeler de dahil olmak üzere eşit aralıklarla yerleştirilecektir. Dolayısıyla, dikdörtgenin her köşesi mutlaka bir lamba konulacak noktadır. Lambalar arasındaki aralığın tüm kenarlarda aynı olması göz önünde bulundurulduğunda, kullanılacak aralık değeri bahçenin çevresini tam bölecek en büyük mesafeye eşit olmak zorundadır ki bu da kenar uzunluklarının hepsine uygun düşmelidir.
Köşeler dahil eşit aralık elde etmenin pratik yöntemi, dikdörtgenin kısa ve uzun kenarlarının ortak bölenlerinden hareketle, kenarların tam katı olacak şekilde bir mesafe seçmektir. Hem 45 hem de 72’yi tam bölen en büyük sayı, 45 ve 72’nin en büyük ortak böleni (EBOB) olarak ifade edilir. Şimdi bu değeri bulalım:
- 45’in asal çarpanları: 3 × 3 × 5
- 72’nin asal çarpanları: 2 × 2 × 2 × 3 × 3
- Ortak asal çarpanlar: 3 × 3 = 9
Dolayısıyla EBOB(45,72) = 9’dur. Bu, kenar başına en uzun aralık mesafesi olarak 9 metrenin kullanılabileceğini gösterir. Diğer bir deyişle lambalar, 9’ar metre aralıkla ve köşelerde de olacak şekilde dizilecektir.
4. Gerekli Toplam Lamba Sayısı
Bahçenin toplam çevresi 234 metredir ve aralık mesafesi 9 metre olduğuna göre, çevredeki toplam aralık sayısı şu şekilde hesaplanır:
Dikdörtgenin etrafını tam bir tur dolaşacak şekilde bakarsak; her aralık, bitişik iki lamba arasındaki mesafedir. Bir çember veya dikdörtgen gibi kapalı şekillerde, “aralık sayısı” aynı zamanda “lamba sayısı” kadardır, çünkü başlangıç ve bitiş noktası birleşir. Dolayısıyla çevre boyunca 26 lamba dikilmesi gerekir.
5. Maliyet Hesaplaması
Aday, bahçeye B lambası (4000 TL adet fiyatı) dikmeye karar vermiştir. Ancak elimizdeki soru, “Eğer aynı bahçeye B lambası yerine A lambası (6000 TL adet fiyatı) dikilseydi, bu ne kadar fazla ödeme olurdu?” şeklindedir.
Bu nedenle öncelikle B lambası için toplam maliyeti, ardından A lambası için toplam maliyeti bulacağız.
5.1 B Lambası Maliyeti
- Birim fiyat = 4000 TL
- Toplam lamba sayısı = 26
- Toplam maliyet = 26 × 4000 = 104 000 TL
5.2 A Lambası Maliyeti
- Birim fiyat = 6000 TL
- Toplam lamba sayısı = 26
- Toplam maliyet = 26 × 6000 = 156 000 TL
6. Farkın Hesaplanması
B lambası kullanan bir kişi toplam 104 000 TL öderken, aynı sayıda A lambası dikse 156 000 TL ödeyecekti. Dolayısıyla aradaki fark:
Bu sonuç, soruda verilen şıklardan 52 000 TL seçeneğiyle uyuşmaktadır. Yani en az ödenecek ekstra miktar 52 000 TL’dir.
7. Özet Tablo
| Aşama | İşlem | Sonuç |
|---|---|---|
| 1. Çevre Hesabı | 2 × (45 + 72) | 234 m |
| 2. Aralık Uzunluğu (EBOB) | EBOB(45,72) = 9 | 9 m |
| 3. Toplam Aralık/Lamba Sayısı | 234 ÷ 9 | 26 |
| 4. B Lambası Toplam Maliyeti | 26 × 4000 TL | 104 000 TL |
| 5. A Lambası Toplam Maliyeti | 26 × 6000 TL | 156 000 TL |
| 6. Maliyet Farkı (A - B) | 156 000 TL − 104 000 TL | 52 000 TL |
Sonuç ve Özet
Bu soruda amaç, dikdörtgen şeklindeki bahçenin her köşesinde ve kenarında eşit uzunlukta aralıklar koruyarak lamba yerleştirmektir. Kenar uzunlukları 45 m ve 72 m olan bir dikdörtgenin çevresi 234 m’dir. Eşit aralığın, 45 ve 72’yi tam bölen en büyük değer olan 9 metre olarak alınması durumunda bahçe etrafına 26 adet lamba dikilir. Lamba tipleri arasında birim fiyat farkı olduğundan, B lambası kullanan bir kişi 104 000 TL öderken, A lambası kullanılsaydı 156 000 TL ödeme yapılacaktı. Aradaki maliyet farkı ise 52 000 TL’dir. Dolayısıyla “en az” ifadesi doğrultusunda cevap 52 000 TL olarak belirlenmektedir.