Rıgjgkhjvjfhf

ORTAOKUL
1

17416136357675101023827834149320
174161363576751010238278341493203264×2448 347 KB

2

Sorunun Çözümü:

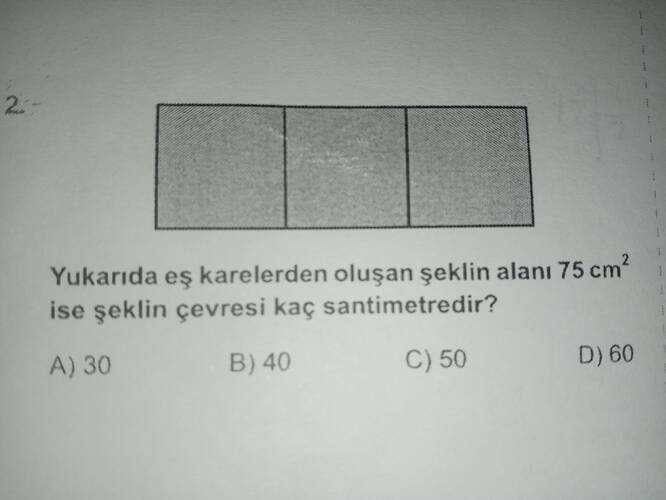
Şekil incelendiğinde: 3 tane eş kareden oluşan bir dikdörtgen verilmiştir. Bu durumda her bir karenin alanını, şeklin toplam alanından yola çıkararak bulabiliriz.

Adım 1: Her Karenin Alanını Bulma

Şeklin toplam alanı = 75 cm² olarak verilmiş. Şekil toplamda 3 kareden oluştuğuna göre bir karenin alanı şu şekilde hesaplanır:

Bir \ Karenin \ Alanı = \frac{Şeklin \ Toplam \ Alanı}{Kare \ Sayısı}
Bir \ Karenin \ Alanı = \frac{75}{3} = 25 \ cm²

Bu durumda her bir karenin alanı 25 cm² olur.

Adım 2: Karenin Kenar Uzunluğunu Bulma

Bir karenin alanı şu şekilde hesaplanır:

Alan = (Kenar \ Uzunluğu)^2

Yukarıda bulduğumuz değer olan 25 cm²’yi, bu formüle koyarak kenar uzunluğunu bulabiliriz:

(Kenar \ Uzunluğu)^2 = 25

Bu denklemden kenar uzunluğu şu şekilde çıkar:

Kenar \ Uzunluğu = \sqrt{25} = 5 \ cm

Bu durumda her bir karenin kenar uzunluğu 5 cm olur.

Adım 3: Şeklin Çevresini Bulma

Şekil, yan yana dizilmiş 3 eş kareden oluştuğuna göre, şeklin toplam çevresi şöyle hesaplanır:

  • Şeklin uzunluğu (3 kare yan yana): Her karenin bir kenarı 5 cm olduğundan, üç karenin toplam uzunluğu:
Uzunluk = 3 \times 5 = 15 \ cm
  • Şeklin genişliği (tek bir kare genişlikte): Karenin bir kenarı olduğu gibi kalır:
Genişlik = 5 \ cm

Şimdi, çevre formülüyle hesaplama yapabiliriz:

Çevre = 2 \times (Uzunluk + Genişlik)
Çevre = 2 \times (15 + 5) = 2 \times 20 = 40 \ cm

Sonuç:

Şeklin çevresi = 40 cm bulunur. Doğru seçenek:
B) 40

Özet Tablo:

Adım Hesaplama Sonuç
Bir karenin alanını bulma ( \frac{75}{3} ) ( 25 , cm^2 )
İlgili kenar uzunluğunu bulma ( \sqrt{25} ) ( 5 , cm )
Çevre hesabı ( 2 \times (15 + 5) ) ( 40 , cm )

Umarım açıklamalar yeterince açıktır! Eğer başka sorularınız olursa sormaktan çekinmeyin. :blush:
@alya3