Bu soruda, her bir arkadaşın satın aldığı ürünlerin fiyatlarına göre sıralama yapmamız isteniyor. Verilen bilgilerden hareketle denklemler kurarak çözümü bulabiliriz.
-
Verilen Bilgiler:
- Mert: 1 tablet (T) ve 1 bilgisayar (B) alıyor.
- Alper: 1 bilgisayar (B) ve 1 cep telefonu (C) alıyor.
- Öykü: 1 tablet (T) ve 1 cep telefonu (C) alıyor.
- Öykü’nün parası Mert’ten az, Alper’den fazla.
-
Denklemler:
- Mert’in parası: T + B
- Alper’in parası: B + C
- Öykü’nün parası: T + C
-
Öncelikli Bilgi:
- T + C < T + B < B + C
-
Sıralama Çözümü:
- T + C < T + B ifadesi, C < B demektir.
- T + B < B + C ifadesi, T < C demektir.
Bu iki ifadeden C < B ve T < C sonucu çıkıyor. Yani:
- T < C < B
Bu durumda doğru seçenek C) T < C < B olacaktır.
Bu şekilde sıralama yapılarak, doğru cevap bulunur.
Bu soruda verilen sıvıların yüzey gerilim değerlerinin sayı kümelerine ait olup olmadığını incelememiz gerekiyor.
-
Sayı Kümeleri:
- Tam Sayılar: Negatif ve pozitif bütünü kapsayan sayılar (…, -2, -1, 0, 1, 2, …).
- Doğal Sayılar: 0 ve pozitif tam sayılar (0, 1, 2, 3, …).
- Rasyonel Sayılar: Kesirli veya tam sayılar, yani a/b şeklinde ifade edilebilen tüm sayılar.
- Gerçek Sayılar: Tüm rasyonel ve irrasyonel sayılar.
-
İnceleme:
- Verilen sıvıların yüzey gerilimleri:
- Etanol: 22,3
- Metanol: 22,6
- Aseton: 23,7
- Asetik Asit: 27,6
- Zeytinyağı: 35,8
- Gliserol: 63,0
- Su: 72,9
- Civa: 486,5
- Verilen sıvıların yüzey gerilimleri:
-
Kümeler Arası Uyumluluk:
- Tam Sayı ve Doğal Sayı olma koşulu için sayının ondalık kısmı olmamalı. (Yalnızca tam kısmı olan sayılar). Bu durumda yalnızca Gliserol (63,0) tam sayıdır.
- Rasyonel Sayı: Bütün verilen sayılar rasyoneldir.
- Gerçek Sayı: Bütün verilen sayılar gerçektir.
Bu bilgilere göre, yüzey gerilim değerinin tam sayı, doğal sayı, rasyonel sayı ve gerçek sayı kümelerinin tamamına uyan tek sıvı Gliseroldür.
Doğru cevap: C) Gliserol.
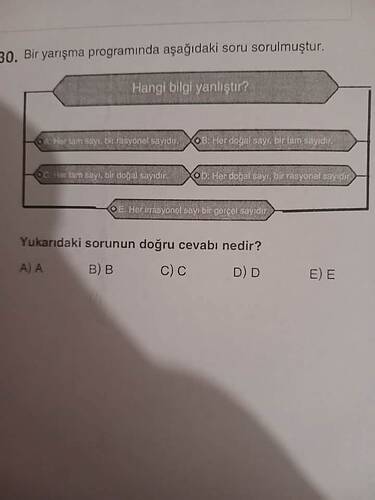
Bu soruda verilen ifadelerden hangisinin yanlış olduğunu bulmamız gerekiyor. Her seçeneği inceleyelim:
-
A) Her tam sayı, bir rasyonel sayıdır.
- Bu doğru bir ifadedir. Her tam sayı n, n/1 şeklinde yazılabilir, bu nedenle rasyoneldir.
-
B) Her doğal sayı, bir tam sayıdır.
- Bu doğru bir ifadedir. Doğal sayılar (0, 1, 2, 3, …) zaten tam sayıların bir alt kümesidir.
-
C) Her tam sayı, bir doğal sayıdır.
- Bu yanlış bir ifadedir. Negatif tam sayılar (örn. -1, -2) doğal sayı değildir.
-
D) Her doğal sayı, bir rasyonel sayıdır.
- Bu doğru bir ifadedir. Her doğal sayı da bir rasyonel sayı şeklinde (n/1) yazılabilir.
-
E) Her irrasyonel sayı, bir gerçek sayıdır.
- Bu doğru bir ifadedir. İrrasyonel sayılar gerçek sayıların bir alt kümesidir.
Yanlış olan ifade C) Her tam sayı, bir doğal sayıdır.
Doğru cevap: C.
Bu soruda verilen üç ifadenin doğruluğunu incelememiz gerekmektedir.
-
I. a < b ise 2a < a + b < 2b
- Bu ifade doğrudur.
- a < b olduğu için, a + a < a + b < b + b yani 2a < a + b < 2b olur.
-
II. a \neq b ise a ile b sayıları arasında sonsuz sayıda gerçek sayı vardır.
- Bu ifade doğrudur.
- İki farklı gerçek sayı arasında her zaman sonsuz sayıda gerçek sayı bulunur.
-
III. a ile b ardışık tam sayılar ise a ile b arasında hiç tam sayı yoktur.
- Bu ifade doğrudur.
- İkisi ardışık tam sayıysa, aralarında başka tam sayı olamaz.
Bu durumda, doğru olan ifadeler: I, II ve III’tür.
Doğru cevap: E) I, II ve III.
Bu soruda, sayı kümelerinin tarihi gelişimi ile ilgili verilen ifadeleri değerlendireceğiz.
-
I. Eski çağlardan itibaren insanlar mevsim ve ay döngülerini takip etmek, avladıkları hayvan sayısının miktarını belirtmek gibi durumlar için mağara duvarlarına veya ağaç gövdelerine attıkları çentiklerden yararlanmışlardır.
- Bu ifade doğrudur. Tarih öncesi dönemlerde insanlar, sayıları ve döngüsel olayları takip etmek için bu tür yöntemleri kullanmışlardır.
-
II. Antik Mısır medeniyetinde yaklaşık 3000 yıl önce sayılar, hiyerogliflerin tekrar edilmesiyle ifade edilmiştir.
- Bu ifade doğrudur. Antik Mısır’da hiyeroglifler, sayısal değerleri belirtmek için kullanılmış ve simgeler tekrar edilerek sayılar oluşturulmuştur.
-
III. Babiller matematikte 60 tabanlı sayı sistemini kullanmıştır.
- Bu ifade doğrudur. Babiller, astronomik hesaplamalarda ve matematikte 60 tabanlı (seksagesimal) sistemi kullanmışlardır.
Bu durumda, üç ifade de doğrudur.
Doğru cevap: E) I, II ve III.
Bu soruda rasyonel sayılarda toplama işlemi ile ilgili verilen ifadelerin doğruluğunu değerlendireceğiz.
-
I. Rasyonel sayılarda \frac{2}{3} kesrinin toplam işlemi göre tersi \frac{3}{2}'dir.
- Bu ifade yanlıştır.
- \frac{2}{3}'ün toplama işlemine göre tersi -\frac{2}{3} olmalıdır.
-
II. Rasyonel sayılar kümesinde toplama işleminin değişme özelliği yoktur.
- Bu ifade yanlıştır.
- Rasyonel sayılar kümesinde toplama işlemi değişme özelliğine sahiptir. Yani a + b = b + a.
-
III. Rasyonel sayılar kümesinde toplama işleminin etkisiz elemanı vardır.
- Bu ifade doğrudur.
- Rasyonel sayılarda toplama işleminin etkisiz elemanı 0'dır çünkü bir sayıyı 0 ile toplamak o sayıyı değiştirmez.
Bu durumda, doğru olan ifade yalnızca III’tür.
Doğru cevap: C) Yalnız III.
Bu soruda, farklı sayı kümelerinin belirli işlemlere göre kapalı olup olmadığını değerlendireceğiz.
-
I. Rasyonel sayılar kümesi toplama işlemine göre kapalıdır.
- Bu ifade doğrudur.
- İki rasyonel sayının toplamı yine bir rasyonel sayıdır. Dolayısıyla, toplama işlemi rasyonel sayılar kümesinde kapalıdır.
-
II. Tam sayılar kümesi çarpma işlemine göre kapalıdır.
- Bu ifade doğrudur.
- İki tam sayının çarpımı yine bir tam sayıdır. Dolayısıyla, çarpma işlemi tam sayılar kümesinde kapalıdır.
-
III. İrrasyonel sayılar kümesi bölme işlemine göre kapalıdır.
- Bu ifade yanlıştır.
- İki irrasyonel sayının bölümü her zaman irrasyonel olmayabilir. Örneğin, \sqrt{2} / \sqrt{2} = 1, bu rasyoneldir. Bu nedenle, bölme işlemi irrasyonel sayılar kümesinde kapalı değildir.
Doğru olan ifadeler I ve II’dir.
Doğru cevap: D) I ve II.