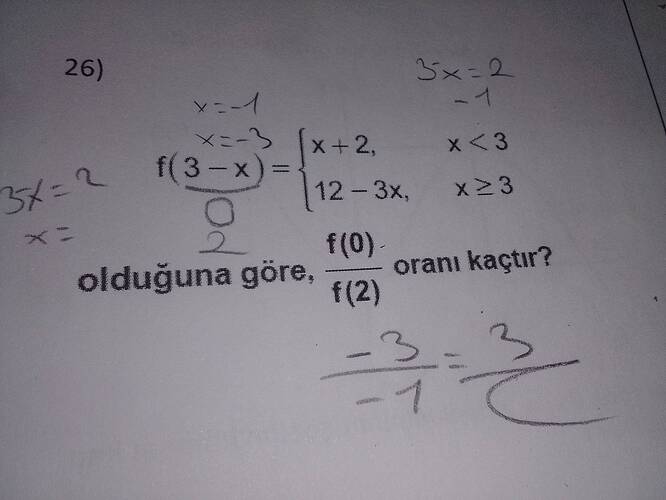Görüntüde bir fonksiyon sorusu yer alıyor. Fonksiyonun iki durumu var:
f(3-x) =
\begin{cases}
x + 2, & x < 3 \\
12 - 3x, & x \geq 3
\end{cases}
Buna göre \frac{f(0)}{f(2)} oranını bulmamız isteniyor.
1. Adım: f(0) Hesaplanması
Öncelikle f(0)'ı bulalım. 3 - x = 0 denklemini çözelim:
3 - x = 0 \implies x = 3
x = 3 durumunda ikinci durumu kullanırız:
f(0) = 12 - 3 \times 3 = 12 - 9 = 3
2. Adım: f(2) Hesaplanması
Şimdi f(2)'yi bulalım. 3 - x = 2 denklemini çözelim:
3 - x = 2 \implies x = 1
x = 1 durumunda birinci durumu kullanırız:
f(2) = 1 + 2 = 3
3. Adım: \frac{f(0)}{f(2)} Oranı
Sonuçları yerine koyarak \frac{f(0)}{f(2)} oranını hesaplayalım:
\frac{f(0)}{f(2)} = \frac{3}{3} = 1
Bu yüzden, istenen oran 1’dir.