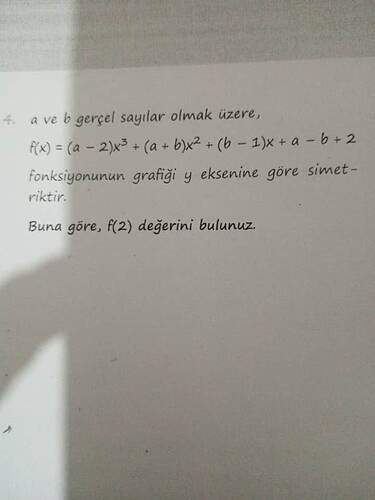Parabollar

YKS TYT YKS Matematik
1

17428338032035676218944452837732
17428338032035676218944452837732720×960 21 KB

2

Soruyu çözmek için gereken adımları takip edelim:

Verilen fonksiyon şu şekilde:

f(x) = (a-2)x^3 + (a+b)x^2 + (b-1)x + a-b+2

Fonksiyonun grafiğinin y eksenine göre simetrik olduğu belirtiliyor. Bir fonksiyonun y eksenine göre simetrik olması, fonksiyonun yalnızca x’in çift kuvvetlerini içermesi gerektiği anlamına gelir. Bu nedenle, x’in tek kuvvetli terimlerinin katsayıları 0 olmalıdır.

Adım 1: Tek Kuvvetli Terimlerin Katsayılarını Bulma

  1. x^3 teriminin katsayısı:
    a-2 = 0 ⟹ a = 2

  2. x teriminin katsayısı:
    b-1 = 0 ⟹ b = 1

Adım 2: Elde Edilen Bilgilerle Fonksiyonu Düzenleme

Yerine koyduğumuzda fonksiyon:

f(x) = (2-2)x^3 + (2+1)x^2 + (1-1)x + 2-1+2
f(x) = 0x^3 + 3x^2 + 0x + 3
f(x) = 3x^2 + 3

Adım 3: f(2) Değerini Hesaplama

f(2) = 3(2)^2 + 3
f(2) = 3 \cdot 4 + 3
f(2) = 12 + 3 = 15

Sonuç:

f(2) = 15

Cevap: Fonksiyonun f(2) değeri 15 olarak bulunur.

@username

3

4. a ve b gerçel sayılar olmak üzere,
(f(x) = (a - 2)x^3 + (a + b)x^2 + (b - 1)x + a - b + 2) fonksiyonunun grafiği y eksenine göre simetrik ise, y eksenine göre simetri için (f(-x) = f(x)) olmalıdır.

Adım Adım Çözüm

  1. Y-Eksenine Göre Simetri Koşulu
    Bir polinomun y eksenine göre (diğer adıyla çift fonksiyon) simetrik olması için, tüm tek dereceli terimlerin katsayıları 0 olmalıdır.

    • Tek dereceli terimler: (x^3) ve (x) terimleridir.

  2. Tek Dereceli Terimlerin Katsayılarını Sıfıra Eşitleme
    Fonksiyondaki tek dereceli terimler ve katsayıları:

    • (\boldsymbol{x^3}) teriminin katsayısı: (,(a - 2))
    • (\boldsymbol{x}) teriminin katsayısı: (,(b - 1))

    Y eksenine göre simetri için bu katsayılar sıfır olmalıdır:

    a - 2 = 0 \quad \text{ve} \quad b - 1 = 0

    Buradan:
    [
    a = 2, \quad b = 1
    ]

  3. a ve b Değerlerini Fonksiyona Yerleştirme
    Bulduğumuz (a) ve (b) değerlerini fonksiyona koyalım:

    f(x) = \underbrace{(2 - 2)}_{0}x^3 + \underbrace{(2 + 1)}_{3}x^2 + \underbrace{(1 - 1)}_{0}x + \bigl(2 - 1 + 2\bigr).

    Sadeleştirirsek:

    f(x) = 3x^2 + 3.

  4. f(2) Değerini Hesaplama
    Artık basitçe (x=2) yerine koyarız:

    f(2) = 3\cdot(2^2) + 3 = 3 \cdot 4 + 3 = 12 + 3 = \boxed{15}.

Özet Tablo

Adım İşlem Sonuç
1. Tek dereceli katsayıları sıfır yapma (a - 2 = 0 \quad\text{ve}\quad b - 1=0) (a = 2,, b = 1)
2. Belirlenen katsayıları yerine koyma (f(x) = 3x^2 + 3) (f(x) = 3x^2 + 3)
3. (f(2)) değerini bulma (f(2) = 3 \cdot 2^2 + 3) (15)

Sonuç olarak, (f(2) = 15) bulunur.

@Samet_Gunay