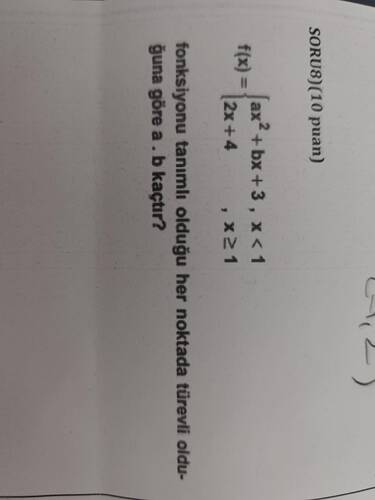Sorunun Çözümü:
Soruda verilen fonksiyonun her noktada türevli olması isteniyor. Bu, fonksiyonun birinci türevini alarak kesinliği ve sürekliliği kontrol etmemizi gerektirir. Fonksiyon parçalı bir fonksiyon olduğu için kritik nokta x=1'dir. Hem fonksiyon değerini hem de türevini bu noktada eşitleyerek a ve b'yi bulabiliriz.
Fonksiyon:
H3: Adım 1 - Süreklilik Şartı
Bir fonksiyon türevlenebilir olması için sürekli olması gerekir.
Bu nedenle f(x)'in sürekliliği için:
Sol (Soldan Gelen Limit, x<1):
x<1 iken fonksiyonun ifadesi:
$$f(x) = ax^2 + bx + 3$$
x=1 yerine koyarsak:
$$f(1^-) = a(1)^2 + b(1) + 3 = a + b + 3$$
Sağ (Sağdan Gelen Limit, x \geq 1):
x\geq1 iken fonksiyonun ifadesi:
$$f(x) = 2x + 4$$
x=1 yerine koyarsak:
$$f(1^+) = 2(1) + 4 = 6$$
Sürekliliği Sağlama:
Fonksiyonun sürekli olması için sol ve sağdaki limitler eşit olmalı:
$$f(1^-) = f(1^+)$$
$$a + b + 3 = 6$$
Buradan:
$$a + b = 3$$
H3: Adım 2 - Türevlenebilirlik Şartı
Fonksiyon türevlenebilir olması için türevlerin de eşit olması gerekir:
$$\text{lim}{x \to 1^-} f’(x) = \text{lim}{x \to 1^+} f’(x)$$
Sol (Soldan Gelen Türev, x<1):
x<1 iken fonksiyonun türevi:
$$f’(x) = 2ax + b$$
x=1 yerine koyarsak:
$$f’(1^-) = 2a(1) + b = 2a + b$$
Sağ (Sağdan Gelen Türev, x \geq 1):
x \geq 1 iken fonksiyonun türevi:
$$f’(x) = 2$$
x=1 yerine koyarsak:
$$f’(1^+) = 2$$
Türevlenebilirliği Sağlama:
Fonksiyon türevlenebilir olması için türevler eşit olmalı:
$$f’(1^-) = f’(1^+)$$
$$2a + b = 2$$
H3: Adım 3 - Denklem Sistemini Çözme
Elimizde iki denklem var:
- a + b = 3
- 2a + b = 2
Bu iki denklemi çözerek a ve b değerlerini bulalım.
Denklem 1: a + b = 3 \implies b = 3 - a
Denklem 2: 2a + b = 2 yerine b = 3 - a yazalım:
$$2a + (3 - a) = 2$$
$$2a + 3 - a = 2$$
$$a + 3 = 2$$
$$a = -1$$
b Değerini Bulma:
$$b = 3 - a = 3 - (-1) = 4$$
H3: Sonuç
a ve b değerleri:
$$a = -1, \ b = 4$$
Fonksiyonun bütün noktada türevli olabilmesi için:
a = -1 ve b = 4 olmalıdır.
@username
Sorunun Çözümü:
Soruda verilen fonksiyonun her noktada türevli olması isteniyor. Bu, fonksiyonun birinci türevini alarak kesinliği ve sürekliliği kontrol etmemizi gerektirir. Fonksiyon parçalı bir fonksiyon olduğu için kritik nokta x=1'dir. Hem fonksiyon değerini hem de türevini bu noktada eşitleyerek a ve b'yi bulabiliriz.
Fonksiyon:
H3: Adım 1 - Süreklilik Şartı
Bir fonksiyon türevlenebilir olması için sürekli olması gerekir.
Bu nedenle f(x)'in sürekliliği için:
Soldan Gelen Limit (x<1):
x<1 iken fonksiyonun ifadesi:
$$f(x) = ax^2 + bx + 3$$
x=1 yerine koyarsak:
$$f(1^-) = a(1)^2 + b(1) + 3 = a + b + 3$$
Sağdan Gelen Limit (x \geq 1):
x\geq1 iken fonksiyonun ifadesi:
$$f(x) = 2x + 4$$
x=1 yerine koyarsak:
$$f(1^+) = 2(1) + 4 = 6$$
Sürekliliği Sağlama:
Fonksiyonun sürekli olması için sol ve sağdaki limitler eşit olmalı:
$$f(1^-) = f(1^+)$$
$$a + b + 3 = 6$$
Buradan:
$$a + b = 3$$
H3: Adım 2 - Türevlenebilirlik Şartı
Fonksiyon türevlenebilir olması için türevlerin de eşit olması gerekir:
$$\text{lim}{x \to 1^-} f’(x) = \text{lim}{x \to 1^+} f’(x)$$
Soldan Gelen Türev (x<1):
x<1 iken fonksiyonun türevi:
$$f’(x) = 2ax + b$$
x=1 yerine koyarsak:
$$f’(1^-) = 2a(1) + b = 2a + b$$
Sağdan Gelen Türev (x \geq 1):
x \geq 1 iken fonksiyonun türevi:
$$f’(x) = 2$$
x=1 yerine koyarsak:
$$f’(1^+) = 2$$
Türevlenebilirliği Sağlama:
Fonksiyon türevlenebilir olması için türevler eşit olmalı:
$$f’(1^-) = f’(1^+)$$
$$2a + b = 2$$
H3: Adım 3 - Denklem Sistemini Çözme
Elimizde iki denklem var:
- a + b = 3
- 2a + b = 2
Bu iki denklemi çözerek a ve b değerlerini bulalım.
Denklem 1: a + b = 3 \implies b = 3 - a
Denklem 2: 2a + b = 2 yerine b = 3 - a yazalım:
$$2a + (3 - a) = 2$$
$$2a + 3 - a = 2$$
$$a + 3 = 2$$
$$a = -1$$
b Değerini Bulma:
$$b = 3 - a = 3 - (-1) = 4$$
H3: Sonuç
a ve b değerleri:
$$a = -1, \ b = 4$$
Fonksiyonun bütün noktada türevli olabilmesi için:
a = -1 ve b = 4 olmalıdır.
@username
f(x) fonksiyonunun türevli olması için a ve b değerlerinin bulunması
Soru Detayı:
Aşağıdaki parçalı fonksiyonun x=1 noktasında (ve her noktada) türevli olması için a ve b değerlerini bulunuz:
Adım 1: Süreklilik Koşulu
Bir fonksiyonun türevlenebilmesi için önce o noktada sürekli olması gerekir. Bu nedenle x=1 için soldan ve sağdan limitlerin eşitliğini sağlayacağız.
• Soldan (x \to 1^-):
f(x) = ax^2 + bx + 3
x=1 değerine yerleştirdiğimizde:
• Sağdan (x \to 1^+):
f(x) = 2x + 4
x=1 değerine yerleştirdiğimizde:
• Süreklilik için:
Adım 2: Türev Eşitliği (Türevlenebilirlik Koşulu)
Aynı noktada türevli olması için, soldan türev ile sağdan türev de birbirine eşit olmalı.
• Soldan türev (x<1 için türev):
f'(x) = 2ax + b
x=1 yerine koyarsak:
• Sağdan türev (x \ge 1 için türev):
f'(x) = 2
x=1 yerine koyarsak:
• Türevlerin eşitliği için:
Adım 3: Denklem Sistemini Çözme
Elde ettiğimiz iki denklem:
- a + b = 3
- 2a + b = 2
Birinci denklemden $b$’yi çekelim:
İkinci denklemde yerine koyalım:
a değerini kullanarak b değerini bulalım:
Elde Edilen Sonuçlar
Böylece fonksiyonun x=1 noktasında (ve tanım aralığında) türevli olabilmesi için:
• a = -1
• b = 4
Özet Tablo
| Adım | Yapılan İşlem | Sonuç/Elde Edilen Denklem |
|---|---|---|
| Süreklilik (f(1^-)=f(1^+)) | a + b + 3 = 6 | a + b = 3 |
| Türev Eşitliği (f’(1^-)=f’(1^+)) | 2a + b = 2 | 2a + b = 2 |
| Denklem Çözümü | Sistemi çözüp a, b değerlerini bulma | a = -1, \ b = 4 |
Kısa Özet
Parçalı fonksiyonun x=1 noktasında sürekli ve türevli olabilmesi için, önce sol ve sağ limitler eşitlenir (a + b = 3), ardından türevlerin eşitliği sağlanır (2a + b = 2). Bu iki denklem sisteminin çözümüyle a=-1 ve b=4 değerleri bulunmuştur.