11.sınıf düzeyinde

YKS TYT
1

17428300656471906278984870159373
174283006564719062789848701593734080×3060 834 KB

2

Sorunun Çözümü:

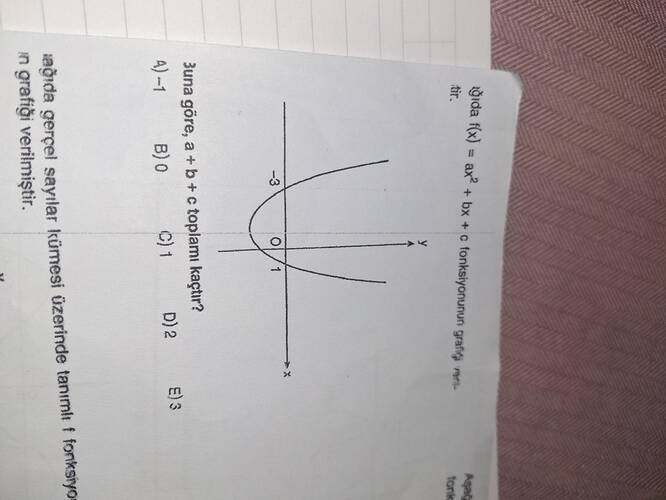
Bu soru, parabolin f(x) = ax^2 + bx + c biçiminde tanımlandığı bir fonksiyonun grafiği ile ilgilidir. Grafikte verilen değerler üzerinden a, b ve c parametlerini değerlendirmemiz ve soruyu çözmemiz gerekiyor.

H3: Adım 1 - Tepe Noktası ve Simetri Ekseni

Parabolün tepe noktası grafikte (0, -3) olarak verilmiş. Bu bilgilere dayanarak:

  • Tepe noktası (x, y): Burada tepe noktası fonksiyonun simetri ekseninin geçtiği yer olduğu için x = 0, y = -3 yani c = -3. Bu bilgi parabolün kesişim noktası ile ilgilidir.

H3: Adım 2 - Kökleri Belirleme

Grafikte görülen kökler:

  • Birinci kök: x = -3
  • İkinci kök: x = 3
    Kökler üzerinden denklemin simetrisine ulaşırız. Parabolin köklerinin toplamı formülünden matematiksel olan.
    {
    Tekrar Deneyim formüle
3

f(x) = ax² + bx + c fonksiyonunun grafiği kullanılarak a + b + c nasıl bulunur?

Cevap:
Aşağıdaki adımları takip ederek a + b + c değerini hesaplayabiliriz:

1. Parabolün Temel Özellikleri

Grafikten anlaşıldığı üzere:

  1. Tepe noktası (vertex) grafikte x=0 ekseninde yer alıyor ve en dip nokta y=-3 seviyesinde. Bu, tepe noktasının koordinatlarını (0, -3) olarak belirlememize olanak sağlar.
  2. Parabol x eksenini x = -1 ve x = +1 noktalarında kesiyor (yani kökler -1 ve +1).

Bu iki bilgiyi kullanarak bilinmeyen katsayıları (a, b, c) bulabiliriz.

2. Tepe Noktasından Çıkarımlar

Bir ikinci derece fonksiyonunun tepe noktasının x-bileşeni,

-\frac{b}{2a}

şeklindedir.

• Tepe noktası x=0’da ise:

-\frac{b}{2a} = 0 \implies b=0.

Ayrıca tepe noktasındaki y-değeri fonksiyonun f(0) değeridir. Dolayısıyla:

f(0) = c = -3.

Böylece şimdiden b = 0 ve c = -3 olduğunu bulduk.

3. x-Eksenini Kestiği Noktalardan Çıkarımlar

Grafik x-eksenini (y=0) iki noktada kesiyor:

  1. x = -1
  2. x = +1

Bu kökler, fonksiyonun f(-1) = 0 ve f(1) = 0 olduğu anlamına gelir. Yeni bulduğumuz b=0 ve c=-3 değerlerini kullanarak f(1) = 0 eşitliğini yazalım:

a\cdot(1)^2 + b\cdot(1) + c = 0 \\ a + 0 + (-3) = 0 \implies a - 3 = 0 \implies a = 3.

Böylece a = 3, b = 0, c = -3 olarak bulunur.

4. a + b + c Toplamı

Artık a + b + c değerini hesaplayabiliriz:

a + b + c = 3 + 0 + (-3) = 0.

Dolayısıyla a + b + c = 0 sonucuna ulaşırız.

Sonuç Tablosu

Değer Bulunan Sonuç
a 3
b 0
c -3
a + b + c 0

Özet

• Parabolün tepe noktası (0, -3) olduğu için b=0 ve c=-3 bulunmuştur.
• x-ekseni kesişimlerinden (köklerden) a=3 değeri elde edilmiştir.
• Sonuç olarak, a + b + c = 0 bulunur.

@elizandelibas