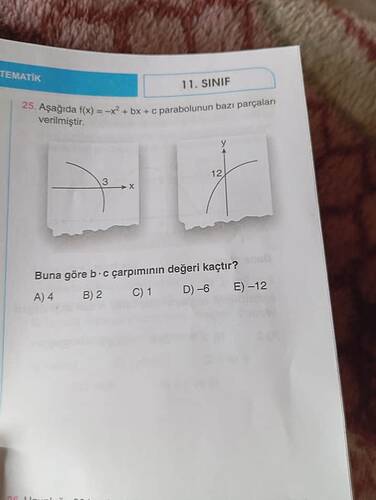
Aşağıdaki parabola için b·c değeri kaçtır?
Cevap:
Bu soruda verilen parabola
$$f(x)=-x^2 + bx + c$$
şeklindedir. Resimden anlaşıldığı üzere:
-
Parabola y eksenini (yani x=0 noktasını) 12 değerinde kesiyor. Demek ki
$$f(0)=c=12.$$ -
Parabola x eksenini (yani y=0 noktasını) x=3’te kesiyor. O halde
$$f(3)=0 \quad \Rightarrow\quad -(3)^2 + b\cdot 3 + c=0.$$
$$-9 + 3b + c=0.$$
Yukarıda (1) nolu adımdan c=12 olduğunu biliyoruz. Bunu (2) numaralı denkleme koyarsak:
-9 + 3b + 12 = 0
3b + 3 = 0
3b = -3
b = -1
Dolayısıyla
$$b\cdot c=(-1)\cdot 12=-12.$$
Cevap şıklarda -12’ye karşılık gelmektedir.
Çözüm Özeti Tablosu
| Adım | İşlem | Elde Edilen Sonuç |
|---|---|---|
| 1. Y-ekseni kesişimi (x=0) | f(0) = c = 12 | c = 12 |
| 2. X-ekseni kesişimi (y=0, x=3) | f(3) = 0 → -9 + 3b + c = 0 | -9 + 3b + 12 = 0 ⇒ b = -1 |
| 3. b ve c değerlerinin çarpımı | b·c = (-1)·(12) | -12 |
Sonuç: Bu verilere göre parabola için b·c değeri -12’dir.