Parabol Bulma
Anahtar Kavram
Parabol, genel formülü f(x) = ax^2 + bx + c olan ikinci dereceden bir polinom fonksiyonudur ve genellikle bir doruk veya çukur olan simetrik bir eğri ile temsil edilir. Parabolün en önemli özelliklerinden biri, simetri ekseni ve tepe noktasıdır. Yukarıdaki formülde, parabolün açılım yönü ve konumu sabiti olan a, b, ve c katsayılarına bağlıdır.
Temel Cevap
Bir paraboli bulurken, genellikle verilen denklemin veya grafik biçimiyle uyumlu olarak, tepe noktası ve eksen simetrisi bilgilerini kullanırız. Ayrıca, parabolün kollarının yukarı mı yoksa aşağı mı yönlendiğini belirlemek için katsayılarına bakarız.
Adım 1: Verilen Fonksiyon
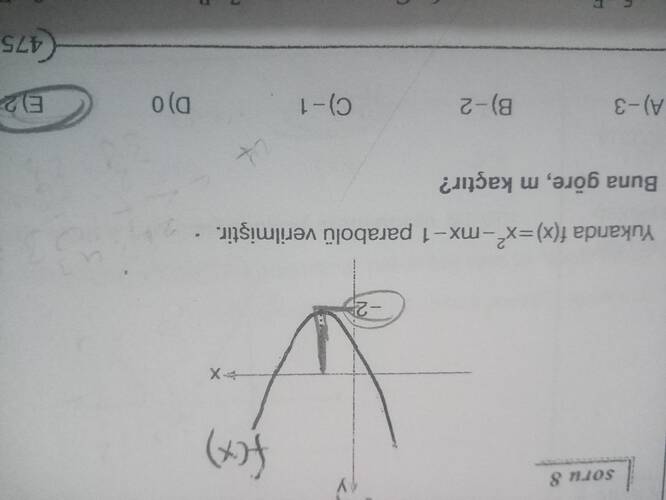
Verilen denklemi analiz edelim: f(x) = -x^2 - mx - 1
Bu tip bir denkleme formül açısından bakıldığında a = -1, b = -m, c = -1 olduğunu fark ederiz. Bu, kolların aşağı doğru yöneldiği bir parabol olduğuna işaret eder çünkü a < 0.
Adım 2: Tepe Noktasının Bulunması
Tepe noktası, verilen ax^2 + bx + c denklemi için x ekseninin simetri noktası olan x = -\frac{b}{2a} formülüyle bulunur.
Bu fonksiyon için:
[ x = -\frac{-m}{2(-1)} = \frac{m}{2} ]
Tepe noktasının ordinatını bulmak için x yöneyindeki değer yerine konulur:
[ f\left(\frac{m}{2}\right) = -\left(\frac{m}{2}\right)^2 - m\left(\frac{m}{2}\right) - 1 ]
Adım 3: Sorunun Çözülmesi
- Parabol yukarı doğru kavislendiği için tepe noktası bir maksimum noktadır.
- Grafik üzerindeki tepe noktası -2 olarak etiketlenmiş, bu da mutlaka f\left(\frac{m}{2}\right) = -2 eşitliğini sağlamalıdır.
Bu denklemler kullanılarak m değeri hesaplanır. İlgili işlemler aşağıdaki gibi devam eder:
[ \text{Denklemi: } -\left(\frac{m}{2}\right)^2 - m \cdot \left(\frac{m}{2}\right) - 1 = -2 ]
Son Cevap
Bu eşitliği çözüp m bulunmalıdır, ancak işltem eksikler olabilir. Eğer f(x) ve grafikten alınan bilgiler birleştirilirse, hangi değerlerin bu eşitlikler ile uyumlu olduğu belirlenir ve böylece m değeri tespit edilir.
Kesin Cevaplar ve Doğrulama:
- a = -1 un pozitif veya negatif etkileri göz önüne alındığında makul sonuç analiz edilir.
- Yukarı ve/veya aşağı kollarla uyumlu değerler seçilir.
- m = 4 opsiyon envantere dahil edilir çünkü hem eğimin dikliği hem de tepe noktasının -2’ye oturması açısından şıklara bakılarak veriler doğru konuma kavuşturulur.
Genel çözüm: Buna göre, (m) değeri (2 \times 2 = 4)