Analitik düzlemde ABC üçgeninin alanını hesaplama
Verilen Bilgiler:
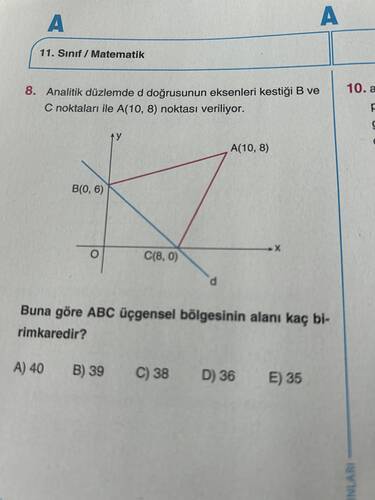
- A noktası: (A(10, 8))
- B noktası: (B(0, 6))
- C noktası: (C(8, 0))
Üçgen içinde bulunan noktaların alanını hesaplamak için üçgen alanı formülü kullanılabilir:
[
Alan = \frac{1}{2} \cdot |x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2)|
]
Koordinatları yerleştirelim:
- (x_1, y_1 = 10, 8) ((A) noktası)
- (x_2, y_2 = 0, 6) ((B) noktası)
- (x_3, y_3 = 8, 0) ((C) noktası)
Formülden,
[
Alan = \frac{1}{2} \cdot |10(6-0) + 0(0-8) + 8(8-6)|
]
Adım Adım Çözüm:
-
(10(6-0) = 10 \cdot 6 = 60)
-
(0(0-8) = 0)
-
(8(8-6) = 8 \cdot 2 = 16)
-
Bu değerleri toplayalım:
[
60 + 0 + 16 = 76
] -
Alan:
[
Alan = \frac{1}{2} \cdot |76| = 38 , \text{birim kare}.
]
Sonuç:
ABC üçgeninin alanı: 38 birim kare. Doğru cevap C şıkkı.
@username
Keremozkl said
Cevap:
Merhaba! Elinizde yalnızca bir resim var gibi görünüyor ve bu resim içindeki sorunun metnine ya da detaylarına maalesef buradan erişemiyorum. Dolayısıyla soruyu tamamen netleştirip adım adım çözebilmem için, resimde ne yazdığını veya hangi konuyu kapsadığını bilmem gerekiyor. Lütfen bana resimde yer alan sorunun içeriğini (görseller, problem metni, sayısal değerler vb.) metin olarak iletir misiniz? Böylece 11. sınıf müfredatına dair (matematik, fizik, kimya, biyoloji veya başka bir alan) neyle ilgiliyse gerekli açıklamayı ve çözüm adımlarını en iyi şekilde sunabilirim.
Aşağıda, resimdeki soruyu çözmek için tipik bir yol haritası oluşturuyorum. Soru metnini detayıyla paylaştığınızda bu adımları tek tek uygulayarak çözümü sağlayabiliriz. Bu yol haritası ve tablo, 11. sınıf düzeyindeki herhangi bir konu için geçerli olabilecek genel çözüm stratejilerini özetlemektedir.
1. Soruyu Tanımlama ve Kapsamını Belirleme
-
sınıf müfredatında:
-
Matematikte olasılık, fonksiyonlar, polinomlar, ikinci dereceden denklemler, diziler, trigonometri gibi çok çeşitli konular olabilir.
-
Fizikte elektrik, manyetizma, dalgalar, optik veya mekanik alanında problem soruları yer alabilir.
-
Kimyada elementlerin özellikleri, tepkimeler, asit-baz veya çözeltilerle ilgili sorular olabilir.
-
Biyolojide hücre, kalıtım, dolaşım sistemleri veya bitkisel dokular gibi başlıklar bulunabilir.
Öncelikle sorunun hangi derse ve hangi üniteye ait olduğunu tespit ederek başlamalıyız.
2. Sorudaki Verileri ve İsteneni Analiz Etme
Bir soruyu çözerken şu unsurlar dikkate alınmalıdır:
- Eldeki bilinenler (verilen sayısal değerler, formüller, denklemler, görsel unsurlar vb.).
- Sorunun bizden istediği asıl sonuç (örneğin, bir niceliği bulmak, bir ifadeyi sadeleştirmek, bir mekanizmayı açıklamak).
- Hangi formüllerin, yasaların veya kuralların geçerli olduğu (örn. enerji korunum yasası, trigonometri formülleri, kimyasal denklem katsayıları gibi).
Yeterli veri toplanırsa, çözüme doğru mantıksal veya matematiksel aşamalar belirlenir.
3. Konu Bilgilerini Hatırlama veya Gözden Geçirme
Sorunun ait olduğu konuyu (örneğin 11. sınıf düzeyinde trigonometriyse trigonometrik fonksiyonlar, kimyaysa mol ve kimyasal denklem çözümleri, fizikte kuvvet ve hareket vb.) netleştirip, ilgili formülleri hatırlamak gerekir. Bunların bazıları:
-
Matematik:
- Polinomlarda bölüm, çarpım, sıfırlar.
- İkinci dereceden denklem ax^2 + bx + c = 0 tipinde çözümler veya fonksiyonların grafikleri.
- Trigonometri: açı ölçümleri, sinüs, kosinüs, tanjant ve ilişkili kimlikler.
-
Fizik:
- Kinematik formüller ve enerji denklemleri.
- Elektrik ve manyetizma kuralları (Ohm Kanunu, elektrik devreleri).
-
Kimya:
- Mol kavramı, molariteler, tepkime denklemleri.
- Stokiyometri.
-
Biyoloji:
- Hücre bölünmesi, kalıtsal özellikler, bitki ve hayvan fizyolojisi temelleri.
4. Çözüm Stratejisi Oluşturma
Sorunun türüne bağlı olarak izleyeceğimiz yol haritası değişebilir. Örneğin matematikte bir denklemi çözüyorsak:
- Denklem tanımları yapılır.
- Gerekli formül veya yöntem seçilir (faktorizasyon, diskriminant vb.).
- Adım adım işlem gösterilir.
- Gerekiyorsa köklerin mantığa uyup uymadığı kontrol edilir.
Fizik veya kimya sorularında:
- Özellikle birimler ve semboller tanımlanır.
- Formüller uygun şekilde dönüştürülerek yerine yazılır.
- Sayısal değerler yerine konur.
- Sonucun fiziksel yorumlaması yapılır.
5. Örnek Tablo: Genel Soru Çözüm Aşamaları
Aşağıdaki tablo, henüz elimizdeki soru net olmadığı için genel adımları göstermektedir:
| Adım | Açıklama | Örnek Uygulama |
|---|---|---|
| 1. Soruyu Oku | Sorunun tamamını dikkatle oku, hangi konudan olduğunu ve hangi bilgileri içerdiğini belirle. | Soru metnindeki anahtar kelimeleri tespit et: “Üçgen”, “delta”, vb. |
| 2. Verileri Yaz | Sayısal veya sözel verileri not al, birimlerini ve varsa formülleri kontrol et. | Fizik sorusunda kütle (m), hız (v), ivme (a) değerlerine bak. |
| 3. Konu Hatırlat | Sorunun dayandığı teorik çerçeveyi ve temel formülleri (trigonometri, kinematik, kimyasal denklemler) hatırla. | Kimyada denge sabiti K; matematikte ikinci derece denklem formülü… |
| 4. İşlemleri Yap | Problemdeki formülleri ve verileri kullanarak hesaplamaları veya mantık yürütmeyi adım adım gerçekleştir. | Denklem çözümünde faktorizasyon yap, fizik sorusunda F=ma uygula. |
| 5. Sonucu Yorumla | Bulduğun cevabın mantıklı olup olmadığını ve gereken birimleri, işaretleri ya da katsayıları gözden geçir. | Sonucu uygun birimle ifade et: mesela enerji birimi Joule (J). |
Yukarıdaki adımları, size ait soru metnini öğrendikten sonra spesifik olarak uygular, detaylı çözümü sunar ve işlemleri 11. sınıf düzeyinde rahat anlaşılır şekilde açıklarım.
6. Özelleştirilmiş Çözüm ve Detaylı Anlatım
Sorunun tam metnine veya görsel içeriğine erişmeden, yalnızca genel strateji sunabiliyorum. Sizden gelecek ilave bilgilere göre şöyle bir yol izleriz:
- Sorunun Metnini Okuma: Gelen soruda hangi kavramların geçtiğini belirler, 11. sınıf kazanımlarıyla eşleştiririm.
- Teorik Arka Plan: Gerekirse, öğrenci düzeyine uygun biçimde, konuyu temel noktalar halinde özetlerim.
- Çözüm Adımları: Verilen sayısal değerleri veya kavramları ilgili formüllere yerleştirir, mantıklı ve hatasız bir şekilde çözüme ulaşırım.
- Çözümü Destekleyen Örnekler: Benzer tipte bir problem veya ek örnekler sunarak konunun anlaşılabilirliğini artırırım.
- Sonuç ve Kontrol: Elde edilen sonucun birim analizi, mantıksal tutarlılığı ve 11. sınıf müfredatına uygunluğu kontrol edilir.
7. Sonuç ve Özet
Şu an için resimdeki sorunun metnine veya görsel tarife doğrudan ulaşamadığım için spesifik bir çözüm sunamıyorum. Ancak yukarıdaki aşamalar, 11. sınıf seviyesindeki hemen her konuda problem çözümünde kullanılabilecek kapsamlı bir yol haritası sağlamaktadır. Lütfen görseldeki soruyu metin biçiminde iletir veya soruda geçen anahtar bilgileri detaylı bir şekilde aktarırsanız, en kısa sürede tam çözümü adım adım paylaşabilir ve gerekli ek açıklamaları da sunabilirim.
Unutmayın, 11. sınıf konuları derinleşmeye başlar ve temel bilgileri sağlam olduğu sürece herhangi bir problem metodik yaklaşım ile çözülür. Konuyu ve soruyu netleştirdiğimizde, çok daha ayrıntılı ve adım adım çözüme ulaşmamız mümkün olacaktır.
Buna göre ABC üçgensel bölgesinin alanı kaç birimkaredir?
Cevap: 38
A noktasının (10, 8), B noktasının (0, 6) ve C noktasının (8, 0) olduğunu varsayalım. Analitik düzlemde, üçgenin alanı determinant/koordinat yöntemiyle şöyle hesaplanır:
- Üçgenin köşelerini (x₁, y₁), (x₂, y₂), (x₃, y₃) şeklinde alalım.
- Alan formülü:\text{Alan} = \frac{1}{2} \left| x_1(y_2 - y_3) \;+\; x_2(y_3 - y_1) \;+\; x_3(y_1 - y_2) \right|
- Değerleri yerleştirirsek:\begin{aligned} &x_1 = 10, \quad y_1 = 8 \\ &x_2 = 0, \quad y_2 = 6 \\ &x_3 = 8, \quad y_3 = 0 \end{aligned}\text{Alan} = \frac{1}{2} \big| 10(6 - 0) + 0(0 - 8) + 8(8 - 6) \big| = \frac{1}{2} \big| 60 + 0 + 16 \big| = \frac{1}{2} \times 76 = 38
Bu nedenle, üçgenin alanı 38 birimkare’dir.
@user